Question

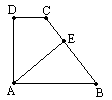
如图，已知AB＝BC，AB∥CD，∠D＝，AE⊥BC．求证：CD＝CE．

Answer 1

答案：
解析：

证明：如图，连结AC，过C作CF⊥AB于F．(这是直角梯形中常见的辅助线) 　　在△CFB和△AEB中， 　　 　　∴△CFB≌△AEB(AAS) 　　∴CF＝AE． 　　∵∠D＝，CF⊥AB且AB∥CD， 　　∴AD＝CF， 　　∴AD＝AE． 　　在Rt△ADC和Rt△AEC中， 　　 　　∴Rt△ADC≌Rt△AEC(HL) 　　∴CD＝CE． 　　思路分析：这是一个直角梯形，通过作CF⊥AB，可以将梯形分成矩形和三角形，结合直角梯形的性质，利用两次全等，达到证明CD＝CE的目的．

提示：

点评：本题主要考查直角梯形、三角形全等的综合运用．在直角梯形中，通过作梯形一底的垂线，将梯形分成特殊的四边形(矩形)和三角形．将题中已知条件AB＝BC中的两条线段AB和BC分别放到两个三角形中，结合直角梯形的性质，利用两次全等，达到证明CD＝CE的目的．解决梯形问题时，除可作以上辅助线外，作一腰的平行线、连对角线、作对角线的平行线也是经常用到的．