

 r
r科目:初中数学 来源: 题型:
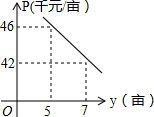 为响应薄熙来书记建设“森林重庆”的号召,某园艺公司从2010年9月开始积极进行植树造林.该公司第x月种植树木的亩数y(亩)与x之间满足y=x+4,(其中x从9月算起,即9月时x=1,10月时x=2,…,且1≤x≤6,x为正整数).由于植树规模扩大,每亩的收益P(千元)与种植树木亩数y(亩)之间存在如图(25题图)所示的变化趋势.
为响应薄熙来书记建设“森林重庆”的号召,某园艺公司从2010年9月开始积极进行植树造林.该公司第x月种植树木的亩数y(亩)与x之间满足y=x+4,(其中x从9月算起,即9月时x=1,10月时x=2,…,且1≤x≤6,x为正整数).由于植树规模扩大,每亩的收益P(千元)与种植树木亩数y(亩)之间存在如图(25题图)所示的变化趋势.查看答案和解析>>
科目:初中数学 来源: 题型:
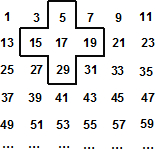 将连续的奇数1,3,5,7,…,排成如下图的数表,用图中所示的十字框可任意框出5个数.
将连续的奇数1,3,5,7,…,排成如下图的数表,用图中所示的十字框可任意框出5个数.查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(四川绵阳卷)数学(带解析) 题型:解答题
如图1,在直角坐标系中,O是坐标原点,点A在y轴正半轴上,二次函数y=ax2+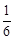 x +c的图象F交x轴于B、C两点,交y轴于M点,其中B(-3,0),M(0,-1)。已知AM=BC。
x +c的图象F交x轴于B、C两点,交y轴于M点,其中B(-3,0),M(0,-1)。已知AM=BC。
(1)求二次函数的解析式;
(2)证明:在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形,并请求出直线BD的解析式;
(3)在(2)的条件下,设直线l过D且分别交直线BA、BC于不同的P、Q两点,AC、BD相交于N。
①若直线l⊥BD,如图1所示,试求 的值;
的值;
②若l为满足条件的任意直线。如图2所示,①中的结论还成立吗?若成立,证明你的猜想;若不成立,请举出反例。
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(四川绵阳卷)数学(解析版) 题型:解答题
如图1,在直角坐标系中,O是坐标原点,点A在y轴正半轴上,二次函数y=ax2+ x
+c的图象F交x轴于B、C两点,交y轴于M点,其中B(-3,0),M(0,-1)。已知AM=BC。
x
+c的图象F交x轴于B、C两点,交y轴于M点,其中B(-3,0),M(0,-1)。已知AM=BC。
(1)求二次函数的解析式;
(2)证明:在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形,并请求出直线BD的解析式;
(3)在(2)的条件下,设直线l过D且分别交直线BA、BC于不同的P、Q两点,AC、BD相交于N。
①若直线l⊥BD,如图1所示,试求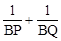 的值;
的值;
②若l为满足条件的任意直线。如图2所示,①中的结论还成立吗?若成立,证明你的猜想;若不成立,请举出反例。

查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省张家港市九年级第一学期调研试卷数学卷 题型:解答题
(本题3分+3分+4分)施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系(如图1所示).
⑴求出这条抛物线的函数解析式,并写出自变量x的取值范围;
⑵隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明;
⑶施工队计划在隧道门口搭建一个矩形“脚手架”CDAB,使A、D点在抛物线上。B、C点在地面OM线上(如图2所示).为了筹备材料,需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少,请你帮施工队计算一下.


|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com