
把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点按顺时针方向旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
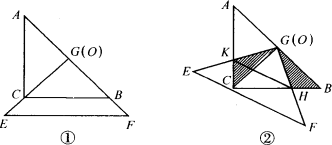
(1)在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论;
(2)连接HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的![]() ?若存在,求出此时x的值;若不存在,说明理由.
?若存在,求出此时x的值;若不存在,说明理由.
|
(1)BH=CK,四边形CHGK的面积不变,∵△ABC为等腰直角三角形,O为其斜边中点, ∴CG=BG,CG⊥AB,∴∠ACG=∠B=45°. 又∵∠BGH与∠CGK均为旋转角,∴∠BGH=∠CGK △BGH≌△CGK,∴BH=CK,S△BGH=S△CGK ∴S四边形CHGK=S△CHG+S△CGK=S△CHG+S△BGH=4 (2)AC=BC=4,BH=x CH=4-x,CK=x ∴S△GKH=S四边形CHGK-S△CHK ∴y=4- ∴y= ∵0°<α<90° ∴0<x<4 (3)存在 ∴x1=1,x2=3 ∴x=1或x=3时,△GHK的面积均等于△ABC的面积的 |


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
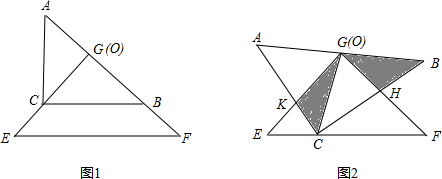
 把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点逆时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点逆时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).| 5 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
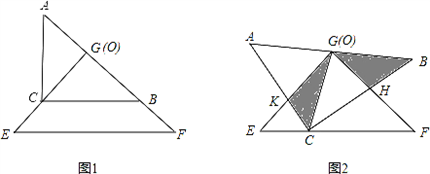
科目:初中数学 来源:云南省期末题 题型:解答题
查看答案和解析>>
科目:初中数学 来源:第25章《图形的变换》常考题集(13):25.2 旋转变换(解析版) 题型:解答题
 ?若存在,求出此时x的值;若不存在,说明理由.
?若存在,求出此时x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:第23章《旋转》常考题集(04):23.1 图形的旋转(解析版) 题型:解答题
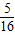 ?若存在,求出此时x的值;若不存在,说明理由.
?若存在,求出此时x的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com