练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

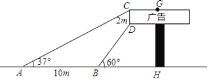
    【题目】如图，长方形广告牌架在楼房顶部，已知CD=2m，经测量得到∠CAH=37°，∠DBH=60°，AB=10m，求GH的长．（参考数据：tan37°≈0.75， ≈1.732，结果精确到0.1m）

    【答案】7.8m．

    【解析】

    首先构造直角三角形，设DE=xm，则CE=（x+2）m，由三角函数得出AE和BE，由AE=BE=AB得出方程，解方程求出DE，即可得出GH的长．

    解：延长CD交AH于点E，如图所示：根据题意得：CE⊥AH， 设DE=xm，则CE=（x+2）m，
    在Rt△AEC和Rt△BED中，tan37°= ，tan60°= ，
    ∴AE= ，BE= ，
    ∵AE﹣BE=AB，
    ∴ ﹣=10，
    即 ﹣=10，
    解得：x≈5.8，
    ∴DE=5.8m，
    ∴GH=CE=CD+DE=2m+5.8m=7.8m．
    答：GH的长为7.8m．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次，每次射耙的成绩情况如图所示：

    （1）请将下表补充完整：（参考公式：方差S2= [（x1﹣）2+（x2﹣）2+…+（xn﹣）2]）

    平均数

    方差

    中位数

    甲

    7

    　 　

    7

    乙

    　 　

    5.4

    　 　

    （2）请从下列三个不同的角度对这次测试结果进行

    ①从平均数和方差相结合看，　 　的成绩好些；

    ②从平均数和中位数相结合看，　 　的成绩好些；

    ③若其他队选手最好成绩在9环左右，现要选一人参赛，你认为选谁参加，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

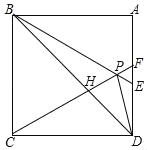
    【题目】如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连接BD、DP，BD与CF相交于点H，给出下列结论：

    ①BE=2AE；②△DFP∽△BPH；③△PFD∽△PDB；④DP2=PHPC

    其中正确的是_____（填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施．调查表明：这种冰箱的售价每降低50元，平均每天就能多售出 4台．商场要想在这种冰箱销售中每天盈利 4800 元，同时又要使百姓得到实惠，每台冰箱应降价多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以△ABC的三边在BC同侧分别作三个等边三角形△ABD，△BCE ，△ACF，试回答下列问题：

    （1）四边形ADEF是什么四边形？请证明：

    （2）当△ABC满足什么条件时，四边形ADEF是矩形？

    （3）当△ABC满足什么条件时，四边形ADEF是菱形？

    （4）当△ABC满足什么条件时，能否构成正方形？

    （5）当△ABC满足什么条件时，无法构成四边形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】新课程改革十分关注学生的社会实践活动，小明在一次社会实践活动中负责了解他所居住的小区500户居民的家庭月人均收入情况，他从中随机调查了40户居民家庭的“家庭月人均收入情况”（收入取整数，单位：元），并绘制了频数分布表和频数分布直方图（如图）．

    分组

    频数

    占比

    1000≤x＜2000

    3

    7.5%

    2000≤x＜3000

    5

    12.5%

    3000≤x＜4000

    a

    30%

    4000≤x＜5000

    8

    20%

    5000≤x＜6000

    b

    c

    6000≤x＜7000

    4

    10%

    合计

    40

    100%

    （1）频数分布表中，a=　 　，b=　 　，C=　 　，请根据题中已有信息补全频数分布直方图；

    （2）观察已绘制的频数分布直方图，可以看出组距是　 　，这个组距选择得　 　（填“好”或“不好”），并请说明理由．

    （3）如果家庭人均月收入“大于3000元不足6000元”的为中等收入家庭，则用样本估计总体中的中等收入家庭大约有　 　户．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

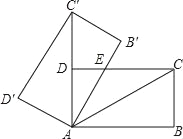
    【题目】如图，将矩形ABCD绕点A旋转至矩形AB′C′D′位置，此时AC′的中点恰好与D点重合，AB′交CD于点E．若AB=6，则△AEC的面积为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC 中，AB＝AC，点 O 是△ABC 的外心，∠BOC＝60°，BC＝2，则 S△ABC＝_

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知等边△ABC，AB=4，以AB为直径的半圆与BC边交于点D，过点D作DE⊥AC，垂足为E，过点E作EF⊥AB，垂足为F，连接FD．

    （1）求证：DE是⊙O的切线；

    （2）求EF的长．

    查看答案和解析>>

    同步练习册答案