
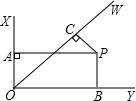
 如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1,则OC=( )
如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1,则OC=( )| A. | 2-$\sqrt{2}$ | B. | $\sqrt{2}-1$ | C. | $\sqrt{6}$-2 | D. | 2$\sqrt{3}$-3 |
分析 先过AP与OW的交点作EF⊥OB,根据已知条件得出∠AEO=∠CEP=45°,再根据sin45°=$\frac{AE}{OE}$=$\frac{CP}{EP}$=$\frac{EF}{OE}$,表示出个边的值,再进行相加,即可得出答案.
解答 解:过AP与OW的交点作EF⊥OB,
∵∠XOY=90°,OW平分∠XOY,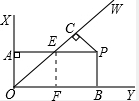
∴∠AOC=∠COB=45°,
∴∠AEO=∠CEP=45°,
∴sin45°=$\frac{AE}{OE}$=$\frac{CP}{EP}$=$\frac{EF}{OE}$,
∴AE=$\frac{\sqrt{2}}{2}$OE,EP=$\sqrt{2}$CP,OE=$\sqrt{2}$EF,
∵cos45°=$\frac{EC}{EP}$,
∴EC=$\frac{\sqrt{2}}{2}$EP,
∵AO=EF,OF+EP=OB,OC=OE+EC,
∴OC=$\sqrt{2}$-1.
故选B.
点评 此题考查了等腰直角三角形,用到的知识点是特殊角的三角函数值,解题的关键是根据角的度数表示出各个边.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
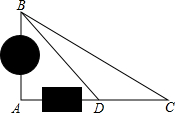 如图,是某社区的一个直角三角形的休闲广场,在直角边AB上修有一处养鱼池,直角边AC上有一个花坛.现测得∠C=30°,从点C沿CA方向前进50米到达点D,测得∠ADB=45°,请你计算AB及AC的长度.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73)
如图,是某社区的一个直角三角形的休闲广场,在直角边AB上修有一处养鱼池,直角边AC上有一个花坛.现测得∠C=30°,从点C沿CA方向前进50米到达点D,测得∠ADB=45°,请你计算AB及AC的长度.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
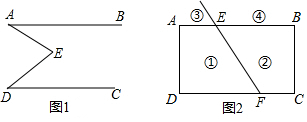 如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
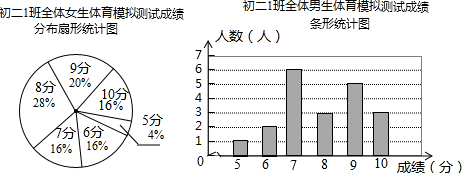
| 平均分 | 方差 | 中位数 | 众数 | |
| 男生 | 7.9 | 2 | 8 | 7 |
| 女生 | 7.92 | 1.99 | 8 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com