
【题目】如图,某中学校园内有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划在中间留一块边长为(a+b)米的正方形地块修建一座雕像,然后将阴影部分进行绿化.

(1)求绿化的面积.(用含a、b的代数式表示)
(2)当a=2,b=4时,求绿化的面积.
科目:初中数学 来源: 题型:
【题目】荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
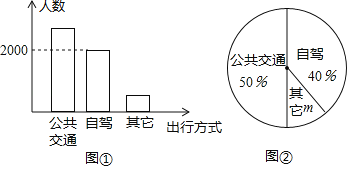
A. 本次抽样调查的样本容量是5000
B. 扇形图中的m为10%
C. 样本中选择公共交通出行的有2500人
D. 若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
查看答案和解析>>
科目:初中数学 来源: 题型:
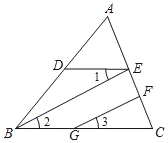
【题目】已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=( )( )
∴DE∥( )( )
∴∠EDB+∠DBC=180°( )
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=( )(已知)
∴∠EDB=180°﹣70°=110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△ADE均为等边三角形,点O是AC的中点,点D在射线BO上,连结OE,EC,则∠ACE=_____°;若AB=1,则OE的最小值=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
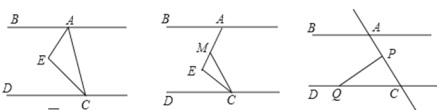
【题目】如图 ,CE 平分∠ACD,AE 平分∠BAC,∠EAC+∠ACE=90°.
(1)请判断 AB 与 CD 的位置关系,并说明理由;
(2)如图,在(1)的结论下,当∠E=90°保持不变时,移动直角顶点 E,使∠MCE=∠ECD, 当直角顶点 E 点移动时,请确定∠BAE 与![]() ∠MCD 的数量关系,并说明理由;
∠MCD 的数量关系,并说明理由;
(3)如图,在(1)的结论下,P 为线段 AC 上的一个定点,点 Q 为直线 CD 上的一个动点,当点 Q 在射线 CD 上运动时(点 C 除外)∠BAC 与∠CPQ+∠CQP 有何数量关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
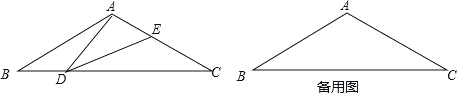
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】CD经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=∠![]() ,
,

(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠![]() =90°,则BE_____CF;EF____
=90°,则BE_____CF;EF____![]() .(填“>”“<”或“=”)
.(填“>”“<”或“=”)
②如图2,若0°<∠BCA<180°,请添加一个关于∠![]() 与∠BCA关系的条件__________,使①中的两个结论仍然成立,并证明两个结论成立.
与∠BCA关系的条件__________,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD经过∠BCA的外部,∠![]() =∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
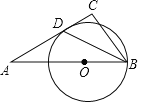
【题目】如图,△ABC中,∠A=30°,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好与AC相切于点D,连接BD.若BD平分∠ABC,AD=2![]() ,则线段CD的长是( )
,则线段CD的长是( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com