
把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12cm,DC=14cm,把三角板DCE绕点C逆时针旋转15°得到△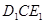 (如图2).这时AB与
(如图2).这时AB与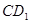 相交于点O,与
相交于点O,与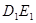 相交于点F.
相交于点F.

(1)填空:∠ = °;
= °;
(2)请求出△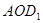 的内切圆半径;
的内切圆半径;
(3)把△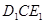 绕着点C逆时针再旋转
绕着点C逆时针再旋转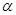 度(
度(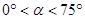 )得△
)得△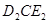 ,若△
,若△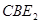 为等腰三角形,求
为等腰三角形,求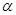 的度数(精确到0.1°).
的度数(精确到0.1°).
(1)120°;(2)2;(3)37.7°、50.6°
【解析】
试题分析:(1)根据旋转的性质结合三角板中的特殊角即可求得结果;
(2)由图可得 度,即可得到AO=6,
度,即可得到AO=6,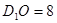 ,
,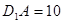 ,根据勾股定理的逆定理可证得△
,根据勾股定理的逆定理可证得△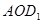 为直角三角形,再根据直角三角形的性质即可求得结果;
为直角三角形,再根据直角三角形的性质即可求得结果;
(3)根据等腰三角形的性质分CB为底边与CB为腰两种情况分析即可.
(1)∠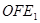 =120°;
=120°;
(2)由题意得 度,AO=6,
度,AO=6,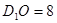 ,
,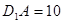
∵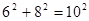
∴△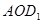 为直角三角形
为直角三角形
∴△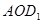 的内切圆半径
的内切圆半径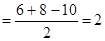 ;
;
(3)由题意当CB为底边时, 的度数为37.7°;当CB为腰时,
的度数为37.7°;当CB为腰时, 的度数为50.6°.
的度数为50.6°.
考点:勾股定理,旋转的性质
点评:能熟练应用勾股定理,利用旋转前后的两个图形完全相等是解题关键.


科目:初中数学 来源: 题型:
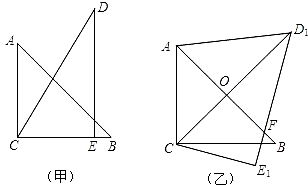 时点B在△D2CE2的内部,外部,还是边上?证明你的判断.
时点B在△D2CE2的内部,外部,还是边上?证明你的判断.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
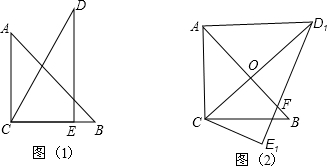
 把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,CD=14,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为
把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,CD=14,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com