
【题目】如图,已知![]() 为
为![]() 的外接圆,
的外接圆,![]() 为
为![]() 的直径,作射线
的直径,作射线![]() ,使得
,使得![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() ,则
,则![]() 的半径为____________.
的半径为____________.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)要证AD是⊙O的切线,连接OA,只证∠DAO=90°即可.
(2)根据三角函数的知识可求出AD,从而根据勾股定理求出AB的长,根据三角函数的知识即可得出⊙O的半径.
(1)证明:连接OA;
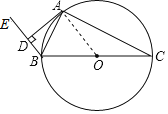
∵BC为⊙O的直径,BA平分∠CBF,AD⊥BF,
∴∠ADB=∠BAC=90°,∠DBA=∠CBA;
∵∠OAC=∠OCA,
∴∠DAO=∠DAB+∠BAO=∠BAO+∠OAC=90°,
∴DA为⊙O的切线.
(2)解:∵BD=1,tan∠ABD=2,
∴AD=2,
∴AB=![]() ,
,
∴cos∠DBA=![]() ;
;
∵∠DBA=∠CBA,
∴BC=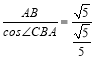 =5.
=5.
∴⊙O的半径为2.5.
故答案为:2.5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
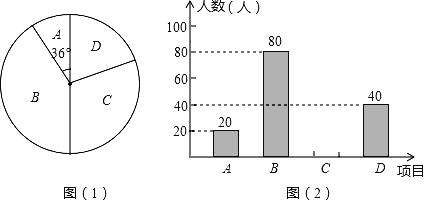
【题目】某中学为了提高学生的综合素质,成立了以下社团A:机器人,B:围棋,C:羽毛球,D:电影配音.每人只能加入一个社团.为了解学生参加社团的情况,从参加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如图两幅不完整的统计图,其中图(1)中A所占扇形的圆心角为36°.
根据以上信息,解答下列问题:
(1)这次被调查的学生共有 人;
(2)请你将条形统计图补充完整;
(3)若该校共有1000学生加入了社团,请你估计这1000名学生中有多少人参加了羽毛球社团.
查看答案和解析>>
科目:初中数学 来源: 题型:
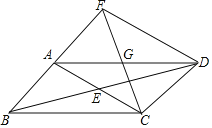
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为全面推进“三供一业”分离移交工作,甲、乙两个工程队承揽了某社区2400米的电路管道铺设工程.已知甲队每天铺设管道的长度是乙队每天铺设管道长度的1.5倍,若两队各自独立完成1200米的铺设任务,则甲队比乙队少用10天.
(1)求甲、乙两工程队每天分别铺设电路管道多少米;
(2)若甲队参与该项工程的施工时间不得超过20天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与坐标轴交于
与坐标轴交于![]() .
.
(1)求抛物线的解析式;
(2)设直线![]() 与该抛物线交于点
与该抛物线交于点![]() (
(![]() 在
在![]() 的左侧),记抛物线在直线
的左侧),记抛物线在直线![]() 下方的图象为
下方的图象为![]() ,在直线
,在直线![]() 下方的图象为
下方的图象为![]() ,将图象
,将图象![]() 沿直线
沿直线![]() 向下翻折得到图象
向下翻折得到图象![]() ,图象
,图象![]() 和图象
和图象![]() 两部分组成的图象记为
两部分组成的图象记为![]() .
.
①设图象![]() 的顶点为
的顶点为![]() ,当
,当![]() 落在
落在![]() 的边上时,求实数
的边上时,求实数![]() 的值.
的值.
②当![]() 时,设
时,设![]() 是图象
是图象![]() 上的动点.
上的动点.
(i)连结![]() ,过线段
,过线段![]() 的中点作
的中点作![]() 轴的平行线交
轴的平行线交![]() 轴于点
轴于点![]() ,当
,当![]() 是以
是以![]() 为直角顶点的直角角形时,直接写出
为直角顶点的直角角形时,直接写出![]() 的值.
的值.
(ii)当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,直接写出
,直接写出![]() 的最大值及相应的
的最大值及相应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
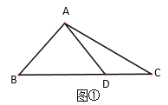
【题目】(问题探究)课堂上老师提出了这样的问题:“如图①,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的一点,
边上的一点,![]() ,求
,求![]() 的长”.某同学做了如下的思考:如图②,过点
的长”.某同学做了如下的思考:如图②,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,进而求解,请回答下列问题:
,进而求解,请回答下列问题:
(1)![]() ___________度;
___________度;
(2)求![]() 的长.
的长.
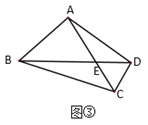
(拓展应用)如图③,在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 相交于点
相交于点![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的长为_____________.
的长为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
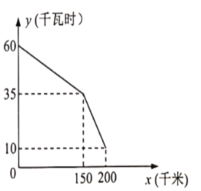
【题目】如图,是某型号新能源纯电动汽车充满电后,蓄电池剩余电量![]() (千瓦时)关于已行驶路程
(千瓦时)关于已行驶路程![]() (千米)的函数图象.
(千米)的函数图象.
(1)根据函数图象,蓄电池剩余电量为35千瓦时汽车已经行驶的路程为____千米.当![]() 时,消耗1千瓦时的电量,汽车能行驶的路程为_____千米.
时,消耗1千瓦时的电量,汽车能行驶的路程为_____千米.
(2)当![]() 时,求
时,求![]() 关于
关于![]() 的函数表达式,并计算当汽车已行驶160千米时,蓄电池的剩余电量.
的函数表达式,并计算当汽车已行驶160千米时,蓄电池的剩余电量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com