
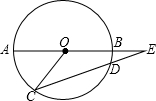
 如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.
如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数. 科目:初中数学 来源: 题型:解答题
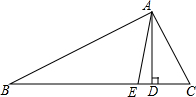 如图,三角形ABC中,∠C>∠B,AD是BC边上的高,AE是三角形中∠A的平分线.
如图,三角形ABC中,∠C>∠B,AD是BC边上的高,AE是三角形中∠A的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
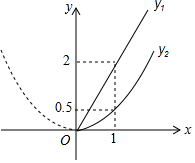 随着成都市近几年城市建设的快速发展,对花木的需求量逐年提高,某园林专业户计划投资种植树木及花卉,根据市场调查与预测,种植树木的利润y1与投入资金x成正比例函数关系;种植花卉的利润y2与投入资金x成二次函数关系,如图所示(利润与投入资金的单位:万元)
随着成都市近几年城市建设的快速发展,对花木的需求量逐年提高,某园林专业户计划投资种植树木及花卉,根据市场调查与预测,种植树木的利润y1与投入资金x成正比例函数关系;种植花卉的利润y2与投入资金x成二次函数关系,如图所示(利润与投入资金的单位:万元)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
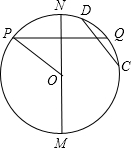 由垂径定理可知:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.请利用这一结论解决问题:
由垂径定理可知:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.请利用这一结论解决问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
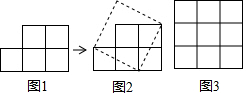
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com