
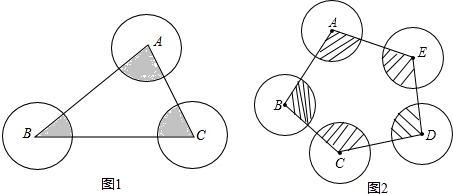
分析 (1)圆心角之和等于五边形的内角和(5-2)×180°=540°,由于半径相同,根据扇形的面积公式S=$\frac{nπ{r}^{2}}{360}$计算即可;
(2)圆心角之和等于n边形的内角和(n-2)×180°,由于半径相同,根据扇形的面积公式S=$\frac{nπ{r}^{2}}{360}$计算即可.
解答 解:(1)五边形ABCDE的内角和(5-2)×180°=540°,
阴影部分的面积之和是$\frac{540×π×{1}^{2}}{360}$=$\frac{3}{2}$π;
(2)n边形的内角和(n-2)×180°,
阴影部分的面积之和S=$\frac{180(n-2)π×{1}^{2}}{360}$=$\frac{n-2}{2}$π.
点评 此题考查扇形的面积计算,正确记忆多边形的内角和公式,以及扇形的面积公式是解决本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 函数图象必经过点(-1,2) | B. | 函数图象经过第二、四象限 | ||
| C. | y随x的增大而增大 | D. | 不论x取何值,总有y>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
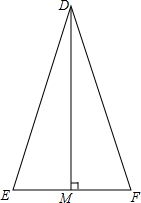 如图所示,在等腰三角形DEF中,腰DE=DF=2$\sqrt{10}$,底边EF=4,DM⊥EF,交EF于点M.
如图所示,在等腰三角形DEF中,腰DE=DF=2$\sqrt{10}$,底边EF=4,DM⊥EF,交EF于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≠-1或x≠-2 | B. | x≠-1 | C. | x≠-2 | D. | x≠-1且x≠-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
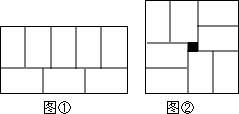 用8块相同的长方形地砖拼矩形,小明拼成了图①,小红拼成了图②,小红所拼图形中间刚好多出一个边长为1的小正方形,则每个小长方形的长宽分别为( )
用8块相同的长方形地砖拼矩形,小明拼成了图①,小红拼成了图②,小红所拼图形中间刚好多出一个边长为1的小正方形,则每个小长方形的长宽分别为( )| A. | 10,6 | B. | 15,9 | C. | 5,3 | D. | 20,12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.86×108 | B. | 8.6×103 | C. | 8.6×107 | D. | 86×102 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com