
【题目】为了满足学生的物质需求,我市某中学到红旗超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表:
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于5200元,且不超5280元,问该红旗超市有几种进货方案?
(3)在(2)的条件下,该红旗超市准备对甲种袋装食品进行优惠促销活动,决定对甲种袋装食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?
【答案】(1)![]() ;(2)共有17种方案;(3)当
;(2)共有17种方案;(3)当![]() 时,
时,![]() 有最大值,即此时应购进甲种绿色袋装食品240袋,表示出乙种绿色袋装食品560袋.
有最大值,即此时应购进甲种绿色袋装食品240袋,表示出乙种绿色袋装食品560袋.
【解析】
(1)根据“用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同”列出方程并解答;
(2)设购进甲种绿色袋装食品x袋,表示出乙种绿色袋装食品(800-x)袋,然后根据总利润列出一元一次不等式组解答;
(3)设总利润为W,根据总利润等于两种绿色袋装食品的利润之和列式整理,然后根据一次函数的增减性分情况讨论求解即可.
解:(1)依题意得:![]()
解得:![]() ,
,
经检验![]() 是原分式方程的解;
是原分式方程的解;
(2)设购进甲种绿色袋装食品![]() 袋,表示出乙种绿色袋装食品
袋,表示出乙种绿色袋装食品![]() 袋,根据题意得,
袋,根据题意得,
![]()
解得:![]() ,
,
∵![]() 是正整数,
是正整数,![]() ,
,
∴共有17种方案;
(3)设总利润为![]() ,则
,则![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 随
随![]() 的增大而增大,
的增大而增大,
所以,当![]() 时,
时,![]() 有最大值,
有最大值,
即此时应购进甲种绿色袋装食品256袋,乙种绿色袋装食品544袋;
②当![]() 时,
时,![]() ,(2)中所有方案获利都一样;
,(2)中所有方案获利都一样;
③当![]() 时,
时,![]() ,
,![]() 随
随![]() 的增大而减小,
的增大而减小,
所以,当![]() 时,
时,![]() 有最大值,
有最大值,
即此时应购进甲种绿色袋装食品240袋,表示出乙种绿色袋装食品560袋.


科目:初中数学 来源: 题型:
【题目】已知点 C为线段 AB上一点,分别以 AC、BC为边在线段 AB同侧作△ACD和△BCE,且 CA=CD,CB=CE,∠ACD=∠BCE,直线 AE与 BD交于点 F
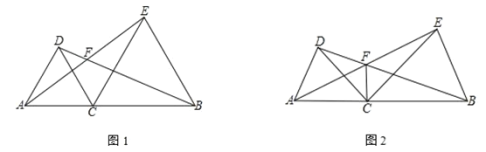
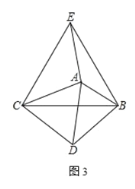
(1)如图 1,若∠ACD=60°,则∠AFD=
(2)如图 2,若∠ACD=α,连接 CF,则∠AFC= (用含α的式子表示)
(3) 将图 1 中的△ACD绕点 C顺时针旋转如图 3,连接 AE、AB、BD,∠ABD=80°,求∠EAB的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() .点
.点![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,以
个单位的速度运动,以![]() 为一边在
为一边在![]() 的右下方作正方形
的右下方作正方形![]() .同时垂直于
.同时垂直于![]() 的直线
的直线![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,设运动时间为
个单位的速度运动,设运动时间为![]() 秒,当
秒,当![]() ________.秒时,直线
________.秒时,直线![]() 和正方形
和正方形![]() 开始有公共点
开始有公共点
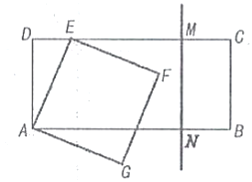
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B、C为数轴上三点,若点C到点A的距离是点C到点B的距离的2倍,则称点C是(A,B)的奇异点,例如图1中,点A表示的数为﹣1,点B表示的数为2,表示1的点C到点A的距离为2,到点B的距离为1,则点C是(A,B)的奇异点,但不是(B,A)的奇异点.
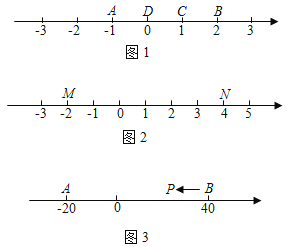
(1)在图1中,直接说出点D是(A,B)还是(B,C)的奇异点;
(2)如图2,若数轴上M、N两点表示的数分别为﹣2和4,
①若(M,N)的奇异点K在M、N两点之间,则K点表示的数是 ;
②若(M,N)的奇异点K在点N的右侧,请求出K点表示的数.
(3)如图3,A、B在数轴上表示的数分别为﹣20和40,现有一点P从点B出发,向左运动.若点P到达点A停止,则当点P表示的数为多少时,P、A、B中恰有一个点为其余两点的奇异点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种盛酒的桶,已知10个大桶加上2个小桶可以盛酒6斛(斛,音hu,是古代的一种容量单位),3个大桶加上15个小桶也可以盛酒6斛.
(1)求1个大桶可盛酒多少斛?
(2)分析2个大桶加上3个小桶可以盛酒2斛吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象分别交
的图象分别交![]() 轴、
轴、![]() 轴于
轴于![]() 、
、![]() 两点,点
两点,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒
方向以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒2个单位长度向点
方向以每秒2个单位长度向点![]() 匀速运动,当其中一点到达终点时,另一点也停止运动,设运动时间为
匀速运动,当其中一点到达终点时,另一点也停止运动,设运动时间为![]() 秒,过点
秒,过点![]() 作
作![]() 轴,连接
轴,连接![]() 、
、![]() .
.
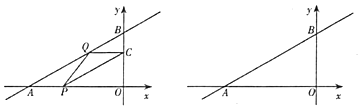
(1)点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,
的坐标为________,![]() ________;
________;
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的值;如果不能,说明理由.
能够成为菱形吗?如果能,求出相应的值;如果不能,说明理由.
(3)若点![]() ,点
,点![]() 在
在![]() 轴上,直线
轴上,直线![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若存在,请直接写出
为顶点的四边形是平行四边形?若存在,请直接写出![]() 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() .
.
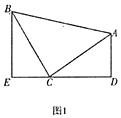
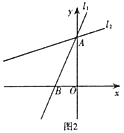
(1)求证:![]() .
.
(2)已知直线![]() 与
与![]() 轴交于
轴交于![]() 点,将直线
点,将直线![]() 绕着
绕着![]() 点顺时针旋转45°至
点顺时针旋转45°至![]() ,如图2,求
,如图2,求![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省城太原某大型超市计划在12月23日推出“十周年”店庆促销活动,该超市为本次促销活动设计了两种促销方案.方案一:全场商品全部打8.5折;方案二:商品总价不超过200元时,不打折,超过200元时,超过的部分打7折.小颖和爸爸妈妈准备在该超市促销活动期间去该超市购物,所购商品总价一定会超过200元.
(1)小颖和爸爸妈妈购买的商品总价为![]() 元,按方案一应该支付 元;按方案二应该支付 元;(用含
元,按方案一应该支付 元;按方案二应该支付 元;(用含![]() 的代数式表示)
的代数式表示)
(2)当小颖和爸爸妈妈购买的商品总价为多少元时,按方案一或方案二支付的金额都一样?
(3)若小颖和爸爸妈妈购买的商品总价为500元,请你帮助小颖计算一下,按哪种方案支付更划算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中进行“选科走班”教学改革,语文、数学、英语三门为必修学科,另外还需从物理、化学、生物、政治、历史、地理(分别记为A、B、C、D、E、F)六门选修学科中任选三门,现对该校某班选科情况进行调查,对调查结果进行了分析统计,并制作了两幅不完整的统计图.
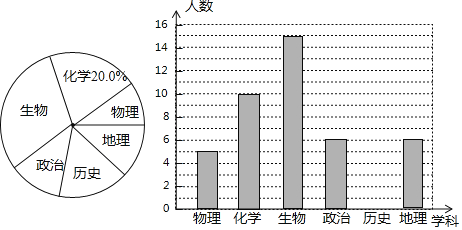
请根据以上信息,完成下列问题:
(1)该班共有学生人;
(2)请将条形统计图补充完整;
(3)该班某同学物理成绩特别优异,已经从选修学科中选定物理,还需从余下选修学科中任意选择两门,请用列表或画树状图的方法,求出该同学恰好选中化学、历史两科的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com