
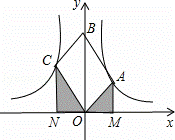
如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y= 和y=
和y= 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
①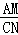 =
=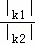 ;
;
②阴影部分面积是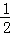 (k1+k2);
(k1+k2);
③当∠AOC=90°时,|k1|=|k2|;
④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
其中正确的结论是 (把所有正确的结论的序号都填上).
①④
解:作AE⊥y轴于E,CF⊥y轴于F,如图,
∵四边形OABC是平行四边形,
∴S△AOB=S△COB,
∴AE=CF,
∴OM=ON,
∵S△AOM=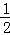 |k1|=
|k1|=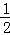 OM•AM,S△CON=
OM•AM,S△CON=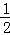 |k2|=
|k2|=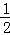 ON•CN,
ON•CN,
∴ =
=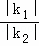 ,所以①正
,所以①正 确;
确;
∵S△AOM=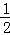 |k1|,S△CON=
|k1|,S△CON=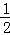 |k2|,
|k2|,
∴S阴影部分=S△AOM+S△CON=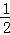 (|k1|+|k2|),
(|k1|+|k2|),
而k1>0,k2<0,
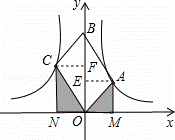
∴S阴影部分=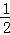 (k1﹣k2),所以②错误;
(k1﹣k2),所以②错误;
当∠AOC=90°,
∴四边形OABC是矩形,
∴不能确定OA与OC相等,
而OM=ON,
∴不能判断△AOM≌△CNO,
∴不能判断AM=CN,
∴不能确定|k1|=|k2|,所以③错误;
若OABC是菱形,则OA=OC,
而OM=ON,
∴Rt△AOM≌Rt△CNO,
∴AM=CN,
∴|k1|=|k2|,
∴k1=﹣k2,
∴两双曲线既关于x轴对称,也关于y轴对称,所以④正确.
故答案为①④.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
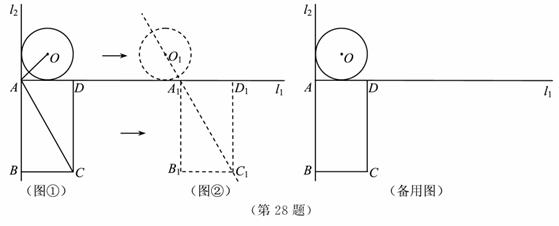
如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为2cm.矩形ABCD的边AD,AB分别 与l1,l2重合,AB=4
与l1,l2重合,AB=4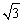 cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).
cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).
(1)如图①,连接OA,AC,则∠OAC的度数为 °;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm).当d<2时,求t的取值范围.(解答时可以利用备用图画出相关示意图)
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题是假命题的是( )
|
| A. | 四个角相等的四边形是矩形 | B. | 对角线相等的平行四边形是矩形 |
|
| C. | 对角线垂直的四边形是菱形 | D. | 对角线垂直的平行四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
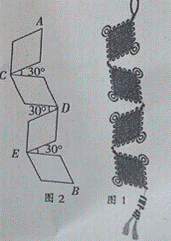
图1中的中国结挂件是由四个相同的菱形在顶点处依次串接而成,每相邻两个菱形均成30度的夹角,示意图如图2所示。在图2中,每个菱形的边长为10cm,锐角为60度。
(1)连接CD、EB,猜想它们的位置关系并加以证明;
(2)求A、B两点之间的距离(结果取整数,可以使用计算器)
(参考 数据:
数据: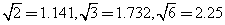 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com