
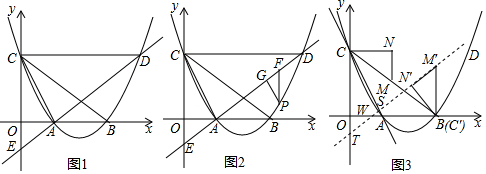
分析 (1)求出A、B、C的坐标,由CD∥AB,推出S△DAB=S△ABC=$\frac{1}{2}$•AB•OC,由此即可解决问题;
(2)首先说明PF的值最大时,△PFG的周长最大,由PF=$\frac{3}{4}$m-$\frac{9}{8}$$\sqrt{3}$-($\frac{\sqrt{3}}{6}$m2-$\frac{11}{4}$m+3$\sqrt{3}$)=-$\frac{\sqrt{3}}{6}$m2+$\frac{7}{2}$m-$\frac{33}{8}$$\sqrt{3}$,可知当m=-$\frac{b}{2a}$=$\frac{7}{2}$$\sqrt{3}$时,PF的值最大,此时P($\frac{7}{2}$$\sqrt{3}$,-$\frac{1}{2}$$\sqrt{3}$),作P关于直线DE的对称点P′,连接P′Q,PQ,作EN∥x轴,QM⊥EN于M,由△QEM∽△EAO,可得$\frac{QM}{QE}$=$\frac{OE}{AE}$=$\frac{3}{5}$,推出QM=$\frac{3}{5}$QE,推出PQ+$\frac{3}{5}$EQ=PQ+QM=P′Q+QM,推出当P′、Q、M共线时,PQ+$\frac{3}{5}$EQ的值最小,想办法求出P′的坐标即可解决问题;
(3)分两种情形①如图3中,当CS=CT时,作CK平分∠OCA,作KG⊥AC于G.由tan∠BWN′=tan∠OCK=$\frac{BN′}{WN′}$,构建方程即可解决问题.②如图4中,当TC=TS时,根据tan∠BWN′=tan∠OAC=$\frac{BN′}{WN′}$,构建方程即可解决问题;
解答 解:(1)令y=0,则2$\sqrt{3}$x2-33x+36$\sqrt{3}$=0,
解得x=$\frac{3\sqrt{3}}{2}$或4$\sqrt{3}$.
∴A($\frac{3\sqrt{3}}{2}$,0),B(4$\sqrt{3}$,0),C(0,3$\sqrt{3}$),
∵CD∥AB,
∴S△DAB=S△ABC=$\frac{1}{2}$•AB•OC=$\frac{1}{2}$×$\frac{5\sqrt{3}}{2}$×$3\sqrt{3}$=$\frac{45}{4}$.
(2)如图2中,设P(m,$\frac{\sqrt{3}}{6}$m2-$\frac{11}{4}$m+3$\sqrt{3}$).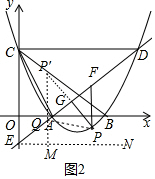
∵A($\frac{3}{2}$$\sqrt{3}$,0),D($\frac{11}{2}\sqrt{3}$,3$\sqrt{3}$),
∴直线AD的解析式为y=$\frac{3}{4}$x-$\frac{9}{8}$$\sqrt{3}$,
∵PF∥y轴,
∴F(m,$\frac{3}{4}$m-$\frac{9}{8}$$\sqrt{3}$),
∵PG⊥DE,
∴△PGF的形状是相似的,
∴PF的值最大时,△PFG的周长最大,
∵PF=$\frac{3}{4}$m-$\frac{9}{8}$$\sqrt{3}$-($\frac{\sqrt{3}}{6}$m2-$\frac{11}{4}$m+3$\sqrt{3}$)=-$\frac{\sqrt{3}}{6}$m2+$\frac{7}{2}$m-$\frac{33}{8}$$\sqrt{3}$,
∴当m=-$\frac{b}{2a}$=$\frac{7}{2}$$\sqrt{3}$时,PF的值最大,此时P($\frac{7}{2}$$\sqrt{3}$,-$\frac{1}{2}$$\sqrt{3}$),
作P关于直线DE的对称点P′,连接P′Q,PQ,作EN∥x轴,QM⊥EN于M,
∵△QEM∽△EAO,
∴$\frac{QM}{QE}$=$\frac{OE}{AE}$=$\frac{3}{5}$,
∴QM=$\frac{3}{5}$QE,
∴PQ+$\frac{3}{5}$EQ=PQ+QM=P′Q+QM,
∴当P′、Q、M共线时,PQ+$\frac{3}{5}$EQ的值最小,
易知直线PP′的解析式为y=-$\frac{4}{3}$x+$\frac{25}{6}$$\sqrt{3}$,
由$\left\{\begin{array}{l}{y=-\frac{4}{3}x+\frac{25}{6}\sqrt{3}}\\{y=\frac{3}{4}x-\frac{9}{8}\sqrt{3}}\end{array}\right.$,可得G($\frac{127}{50}$$\sqrt{3}$,$\frac{39}{50}$$\sqrt{3}$),
∵PG=GP′,
∴P′($\frac{79}{50}$$\sqrt{3}$,$\frac{103}{50}$$\sqrt{3}$),
∴P′M=$\frac{103}{50}$$\sqrt{3}$+$\frac{9}{8}$$\sqrt{3}$=$\frac{637}{200}$$\sqrt{3}$,
∴PQ+$\frac{3}{5}$EQ的最小值为$\frac{637}{200}$$\sqrt{3}$.
(3)①如图3中,当CS=CT时,作CK平分∠OCA,作KG⊥AC于G.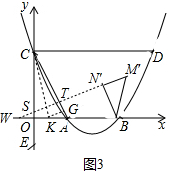
易知KO=KG,
∵$\frac{{S}_{△COK}}{{S}_{△CAK}}$=$\frac{OK}{KA}$=$\frac{\frac{1}{2}•OC•OK}{\frac{1}{2}•AC•KG}$=$\frac{OC}{AC}$=$\frac{2}{\sqrt{5}}$,
∴OK=$\frac{2}{2+\sqrt{5}}$•$\frac{3\sqrt{3}}{2}$=3$\sqrt{15}$-6$\sqrt{3}$,
易证∠BWN′=∠OCK,
∴tan∠BWN′=tan∠OCK=$\frac{BN′}{WN′}$=$\frac{3\sqrt{15}-6\sqrt{3}}{3\sqrt{3}}$,
∵BN′=2$\sqrt{3}$,
∴WN′=2$\sqrt{15}$+4$\sqrt{3}$.
②如图4中,当TC=TS时,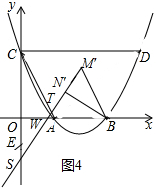
易证∠BWN′=∠OAC,
∴tan∠BWN′=tan∠OAC=$\frac{BN′}{WN′}$=$\frac{3\sqrt{3}}{\frac{3\sqrt{3}}{2}}$,
∴WN′=$\sqrt{3}$,
综上所述,满足条件的WN′的长为2$\sqrt{15}$+4$\sqrt{3}$或$\sqrt{3}$.
点评 本题考查二次函数综合题、一次函数的应用、待定系数法、相似三角形的判定和性质、垂线段最短、轴对称变换、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,学会构建一次函数解决交点坐标问题,学会利用锐角三角函数构建方程解决问题,属于中考压轴题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
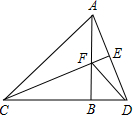 如图所示,△ABC,△BDF为等腰直角三角形,AB⊥CD,点F在线段AB上,延长CF交AD于点E.
如图所示,△ABC,△BDF为等腰直角三角形,AB⊥CD,点F在线段AB上,延长CF交AD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在8×8的正方形网格中的每个小正方形边长都是1,线段交点称做格点.任意连接这些格点,可得到一些线段.按要求画图:
如图,在8×8的正方形网格中的每个小正方形边长都是1,线段交点称做格点.任意连接这些格点,可得到一些线段.按要求画图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com