
【题目】已知抛物线y=ax2+bx+c的顶点为(1,0),且经过点(0,1).
(1)求该抛物线对应的函数的解析式;
(2)将该抛物线向下平移m(m>0)个单位,设得到的抛物线的顶点为A,与x轴的两个交点为B、C,若△ABC为等边三角形.
①求m的值;
②设点A关于x轴的对称点为点D,在抛物线上是否存在点P,使四边形CBDP为菱形?若存在,写出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:由题意可得, 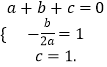 ,解得
,解得 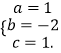 ,
,
故抛物线对应的函数的解析式为y=x2﹣2x+1
(2)
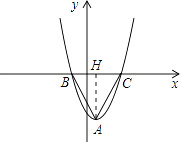
解:①将y=x2﹣2x+1向下平移m个单位得:y=x2﹣2x+1﹣m=(x﹣1)2﹣m,
令y=x2﹣2x+1﹣m=(x﹣1)2﹣m=0,
解得x=1﹣ ![]() 或x=1+
或x=1+ ![]() ,
,
可知A(1,﹣m),B(1﹣ ![]() ,0),C(1+
,0),C(1+ ![]() ,0),BC=2
,0),BC=2 ![]() ,
,
过点A作AH⊥BC于H,
∵△ABC为等边三角形,
∴BH=HC= ![]() BC,∠CAH=30°,
BC,∠CAH=30°,
∴AH= ![]() ,即
,即 ![]() =m,
=m,
由m>0,解得m=3.
②在抛物线上存在点P,能使四边形CBDP为菱形.理由如下:
∵点D与点A关于x轴对称,
∴D(1,3),
①当DP为对角线时,显然点P在点A位置上时,符合题意,
故此时点P坐标为(1,﹣3);
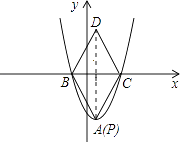
②当DP为边时,要使四边形CBDP为菱形,需DP∥BC,DP=BC.
由点D的坐标为(1,3),DP=BC=2 ![]() ,可知点P的横坐标为1+2
,可知点P的横坐标为1+2 ![]() ,
,
当x=1+2 ![]() 时,y=x2﹣2x+1﹣m=x2﹣2x﹣2=
时,y=x2﹣2x+1﹣m=x2﹣2x﹣2= ![]() ﹣2(1+2
﹣2(1+2 ![]() )﹣2=11≠3,
)﹣2=11≠3,
故不存在这样的点P.
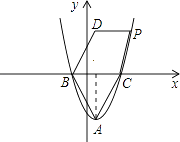
综上可得,存在使四边形CBDP为菱形的点P,坐标为(1,﹣3).
【解析】(1)根据抛物线的顶点坐标及函数经过点(0,1),利用待定系数法求解即可.(2)①先写出平移后的函数解析式,然后得出A、B、C三点的坐标,过点A作AH⊥BC于H,根据△ABC为等边三角形,可得出关于m的方程,解出即可;②求出点D坐标,分两种情况进行讨论,①PD为对角线,②PD为边,根据菱形的性质求解即可.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).


科目:初中数学 来源: 题型:
【题目】解方程
①(x﹣3)﹣3(3x﹣1)=1
②老师在黑板上出了一道解方程的题![]() =1﹣
=1﹣![]() ,小明马上举手,要求到黑板上做,他是这样做的:
,小明马上举手,要求到黑板上做,他是这样做的:
4(2x﹣1)=1﹣3(x+2)…①
8x﹣4=1﹣3x﹣6…②
8x+3x=1﹣6+4…③
11x=﹣1…④
x=﹣![]() …⑤
…⑤
老师说:小明解一元一次方程的一般步骤都知道却没有掌握好,因此解题时有一步出现了错误,请你指出他错在那一步(填编号),并写出正确的解答过程.
![]() =1﹣
=1﹣![]()
③当m为何值时,关于x的方程5m+3x=1+x的解比关于x的方程2x+m=3m的解小2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1。在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换。若骰子的初始位置为图1所示的状态,那么按上述规则连续完成14次变换后,骰子朝上一面的点数是_____________________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角板ABC的两直角边AC,BC的长分别是40cm和30cm,点G在斜边AB上,且BG=30cm,将这个三角板以G为中心按逆时针旋转90°,至△A′B′C′的位置,那么旋转后两个三角板重叠部分(四边形EFGD)的面积为cm2 . 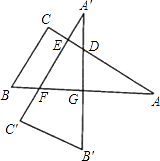
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B是数轴上的点,且点A表示数-3,请参照图并思考,完成下列各题:
![]()
(1)将A点向右移动4个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是 .
(2)若把数轴绕点A对折,则对折后,点B落在数轴上的位置所表示的数为 .
(3)若(1)中点B以每秒2个单位长度沿数轴向左运动,A不动,多长时间后,点B与点A距离为2个单位长度?试列式计算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11分)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.
(1)在点P(1,2),Q(2,-2),N(![]() ,-1)中,是“垂点”的点为 ;
,-1)中,是“垂点”的点为 ;
(2)点M(-4,m)是第三象限的“垂点”,直接写出m的值 ;
(3)如果“垂点矩形”的面积是![]() ,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG的边上存在“垂点”时,GE的最小值为8.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有三个分别写有数字﹣1,0,1的乒乓球(形状,大小一样),先从盒子里随即取出一个乒乓球,记下数字后放回盒子,摇匀后再随即取出一个乒乓球,记下数字.
(1)请用树状图或列表的方法求两次取出乒乓球上数字相同的概率;
(2)求两次取出乒乓球上数字之积等于0的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 ![]() 的值为( )
的值为( ) 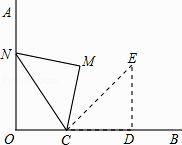
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com