
关于x的一元二次方程x2-mx+5(m-5)=0的两个正实数根 分别为x1、x2,且2x1+x2=7,则m的值是( )
分别为x1、x2,且2x1+x2=7,则m的值是( )
A.-2 B.6 C.2或6 D.7
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
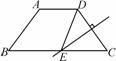
如图,梯形ABCD中,AD∥B C,AD=3,AB=5,BC=9,CD的垂直平分线交BC于E,连结DE,则四边形ABED的周长等于( )
C,AD=3,AB=5,BC=9,CD的垂直平分线交BC于E,连结DE,则四边形ABED的周长等于( )
A.17 B.18 C.19 D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
随着人民生活水平的不断提高,萧山区家庭轿车的拥有量逐年增加.据统计,某小区2007年底拥有家庭轿车81辆,2009年底家庭轿车的拥有量达到144辆.
(1)若该小区2007年底到2009年底家庭轿车拥有量的年平均增长率都相同,求该小区到2010年底家庭轿车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资25万元再建造若干个停车位.据测算,建造费用分别为室内车位6000元/个,露天车位2000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的3倍,但不超过室内车位的4.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com