
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
![]()
(1)若AC=9cm,CB=6cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC-BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并直接写出你的结论.
【答案】(1)MN=7.5cm;(2)MN=![]() acm;(3)
acm;(3)![]() bcm.
bcm.
【解析】
(1)根据“点M、N分别是AC、BC的中点”,先求出MC、CN的长度,再利用MN=CM+CN即可求出MN的长度即可,
(2)当C为线段AB上一点,且M,N分别是AC,BC的中点,则存在MN= ![]() ,
,
(3)点在AB的延长线上时,根据M、N分别为AC、BC的中点,即可求出MN的长度.
(1)∵AC=9cm,点M是AC的中点,
∴CM=0.5AC=4.5cm,
∵BC=6cm,点N是BC的中点,
∴CN=0.5BC=3cm,
∴MN=CM+CN=7.5cm,
∴线段MN的长度为7.5cm,
(2)MN= ![]() a,
a,
当C为线段AB上一点,且M,N分别是AC,BC的中点,则存在MN= ![]() a,
a,
(3)当点C在线段AB的延长线时,如图:![]()
则AC>BC,
∵M是AC的中点,
∴CM= ![]() AC,
AC,
∵点N是BC的中点,
∴CN= ![]() BC,
BC,
∴MN=CM-CN= ![]() (AC-BC)=
(AC-BC)= ![]() b.
b.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .求
.求![]() 的度数;
的度数;
请补全下列解法中的空缺部分.
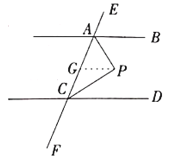
解:过点![]() 作
作![]() 交
交![]() 于点
于点![]()
∵![]() (___________)
(___________)
∴_________![]() (___________)
(___________)
∵![]() (___________)
(___________)
∴![]() ___________(___________)
___________(___________)
且![]() ______________(平行于同一直线的两直线也互相平行)
______________(平行于同一直线的两直线也互相平行)
∴![]() ____________(两直线平行,内错角相等)
____________(两直线平行,内错角相等)
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
∴![]() _____________,
_____________,
![]() _________________.(___________)
_________________.(___________)
∴![]() (___________)
(___________)
∴![]()
总结:两直线平行时,同旁内角的角平分线_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,过点B做射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,连接DF,设运动的时间为t秒(t>0).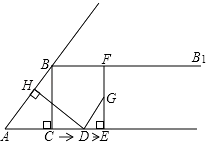
(1)当t为时,AD=AB,此时DE的长度为;
(2)当△DEF与△ACB全等时,求t的值;
(3)以DH所在直线为对称轴,线段AC经轴对称变换后的图形为A′C′.
①当t> ![]() 时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
③当线段A′C′与射线BB1有公共点时,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的4月23日是“世界读书日”.某中学为了了解八年级学生的读书情况,随机调查了50名学生的册数,统计数据如表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
则这50名学生读数册数的众数、中位数是( )
A.3,3
B.3,2
C.2,3
D.2,2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com