
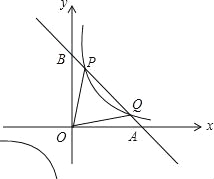
【题目】已知直线y=kx+b与x轴、y轴分别交于A、B两点,与反比例函数交于一象限内的P(![]() ,n),Q(4,m)两点,且tan∠BOP=
,n),Q(4,m)两点,且tan∠BOP=![]() :
:
(1)求反比例函数和直线的函数表达式;
(2)求△OPQ的面积.
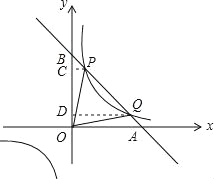
【答案】(1)直线的函数表达式为y=﹣2x+9;(2)![]() .
.
【解析】
试题分析:(1)过P作PC⊥y轴于C,由P(![]() ,n),得到OC=n,PC=
,n),得到OC=n,PC=![]() ,根据三角函数的定义得到P(
,根据三角函数的定义得到P(![]() ,8),于是得到反比例函数的解析式为y=
,8),于是得到反比例函数的解析式为y=![]() ,Q(4,1),解方程组即可得到直线的函数表达式为y=﹣2x+9;
,Q(4,1),解方程组即可得到直线的函数表达式为y=﹣2x+9;
(2)过Q作OD⊥y轴于D,于是得到S△POQ=S四边形PCDQ=![]() .
.
试题解析:(1)过P作PC⊥y轴于C,∵P(![]() ,n),∴OC=n,PC=
,n),∴OC=n,PC=![]() ,
,
∵tan∠BOP=![]() ,∴n=8,∴P(
,∴n=8,∴P(![]() ,8),设反比例函数的解析式为y=
,8),设反比例函数的解析式为y=![]() ,
,
∴a=4,∴反比例函数的解析式为y=![]() ,∴Q(4,1),
,∴Q(4,1),
把P(![]() ,8),Q(4,1)代入y=kx+b中得
,8),Q(4,1)代入y=kx+b中得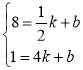 ,∴
,∴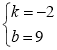 ,
,
∴直线的函数表达式为y=﹣2x+9;
(2)过Q作OD⊥y轴于D,则S△POQ=S四边形PCDQ=![]() (
(![]() +4)×(8﹣1)=
+4)×(8﹣1)=![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】在下列事件中,是必然事件的是
A. 买一张电影票,座位号一定是偶数
B. 随时打开电视机,正在播新闻
C. 将△ACB绕点C旋转50°得到△A′C′B′,这两个三角形全等
D. 阴天就一定会下雨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分)的变化示意图.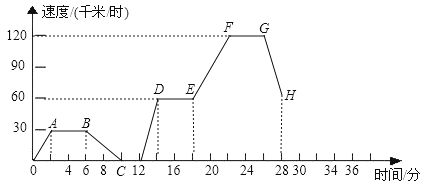
(1)从点A到点B、点E到点F、点G到点H分别表明汽车在什么状态?
(2)汽车在点A的速度是多少?在点C呢?
(3)司机在第28分钟开始匀速先行驶了4分钟,之后立即以减速行驶2分钟停止,请你在本图中补上从28分钟以后汽车速度与行驶时间的关系图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1: ![]() ,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留一位小数,
,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留一位小数, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.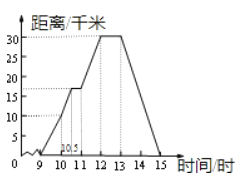
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com