
【题目】如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角.关于这七个角的度数关系,下列何者正确( )
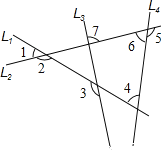
A. ∠2=∠4+∠7 B. ∠3=∠1+∠6 C. ∠1+∠4+∠6=180° D. ∠2+∠3+∠5=360°
【答案】C
【解析】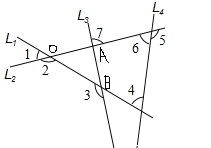
A项,根据三角形外角的性质可知,∠2=∠4+∠6,因为L3和L4不平行,所以∠6≠∠7,所以∠2≠∠4+∠7,故A项错误;
B项,根据三角形外角的性质可知,∠3=∠AOB+∠OAB,根据对顶角相等可知,∠1=∠AOB,∠7=∠OAB,所以∠3=∠1+∠7,因为L3和L4不平行,所以∠7≠∠6,所以∠3≠∠1+∠6,故B项错误;
C项,根据三角形内角和定理可知,∠AOB+∠4+∠6=180°,又根据对顶角相等可知,∠1=∠AOB,所以∠1+∠4+∠6=180°,故C项正确;
D项,根据三角形外角的性质可知,∠2=∠4+∠6,又因为∠5+∠6=180°,所以∠2+∠3+∠5=∠4+∠6+∠3+∠5=∠3+∠4+180°,因为L3和L4不平行,所以∠3+∠4≠180°,所以∠2+∠3+∠5≠360°,故D项错误.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,在直线![]() 上,线段
上,线段![]() ,动点
,动点![]() 从
从![]() 出发,以每秒2个单位长度的速度在直线
出发,以每秒2个单位长度的速度在直线![]() 上运动.
上运动.![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,设点
的中点,设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
![]()
(1)若点![]() 在线段
在线段![]() 上的运动,当
上的运动,当![]() 时,
时,![]() ________;
________;
(2)若点![]() 在射线
在射线![]() 上的运动,当
上的运动,当![]() 时,求点
时,求点![]() 的运动时间
的运动时间![]() 的值;
的值;
(3)当点![]() 在线段
在线段![]() 的反向延长线上运动时,线段AB、PM、PN有怎样的数量关系?请写出你的结论,并说明你的理由.
的反向延长线上运动时,线段AB、PM、PN有怎样的数量关系?请写出你的结论,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程(x+1)(x﹣2)=10根的情况是( )
A. 无实数根 B. 有两个正根
C. 有两个根,且都大于﹣1 D. 有两个根,其中一根大于2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在今年对全市6000名八年级学生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
组别 | 视力 | 频数(人) |
|
| 20 |
|
|
|
|
|
|
|
| 70 |
|
| 10 |
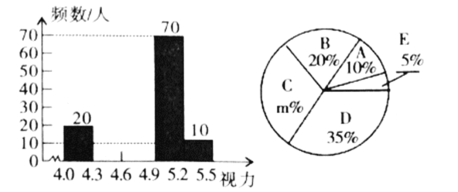
请根据图表信息回答下列问题:
(1)求抽样调查的人数;
(2)![]() ___________,
___________,![]() _____________,
_____________,![]() _____________;
_____________;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展了“手机伴我健康行”主题活动.他们随机抽取部分学生进行“手机使用目的”和“每周使用手机时间”的问卷调查,并绘制成如图①②的统计图。已知“查资料”人人数是40人。
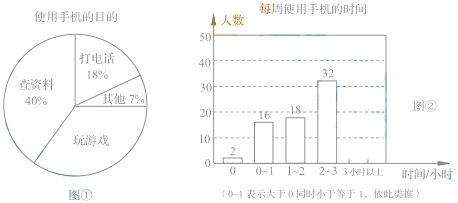
请你根据以上信息解答以下问题
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是_______________。
(2)补全条形统计图
(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了估计鱼塘中成品鱼(个体质量在0.5 kg及以上,下同)的总质量,先从鱼塘中捕捞50条成品鱼,称得它们的质量如下表:

然后做上记号再放回鱼塘中,过几天又捕捞了100条成品鱼,发现其中2条带有记号.
(1)请根据表中数据补全下面的直方图(各组中数据包括左端点不包括右端点);

(2)根据图中数据分组,估计从鱼塘中随机捕一条成品鱼,其质量落在哪一组的可能性最大?
(3)根据图中数据分组,估计鱼塘里质量中等的成品鱼,其质量落在哪一组内?
(4)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1 kg).
查看答案和解析>>
科目:初中数学 来源: 题型:
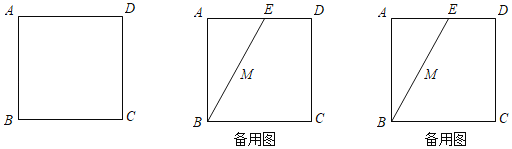
【题目】如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°.
(1)利用尺规作图(保留作图痕迹):分别以点B、C为圆心,BC长为半径作弧交正方形内部于点T,连接BT并延长交边AD于点E,则∠AEB=60°;
(2)在前面的条件下,取BE中点M,过点M的直线分别交边AB、CD于点P、Q.
①当PQ⊥BE时,求证:BP=2AP;
②当PQ=BE时,延长BE,CD交于N点,猜想NQ与MQ的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是长方形,四边形AEFG是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若∠BCF=30°,CD=4,CF=6,则正方形AEFG的面积为( )
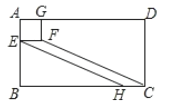
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com