
 在梯形ABCD中,AD∥BC,又$\frac{AD}{BC}$=$\frac{1}{2}$,点M在边AB,且使$\frac{AM}{MB}$=$\frac{2}{3}$,点N在边CD上,使线段MN把梯形分成面积比为3:1的两部分,求$\frac{CN}{ND}$的值.
在梯形ABCD中,AD∥BC,又$\frac{AD}{BC}$=$\frac{1}{2}$,点M在边AB,且使$\frac{AM}{MB}$=$\frac{2}{3}$,点N在边CD上,使线段MN把梯形分成面积比为3:1的两部分,求$\frac{CN}{ND}$的值. 分析 作出辅助线连结MC,MD,过M作梯形的高GH,分两种情况:①当S四边形AMND:S四边形BCNM=1:3时,②当S四边形AMND:S四边形BCNM=3:1时分别求解即可.
解答 解:如图,连结MC,MD,过M作梯形的高GH,分别交AD的延长线,BC于点G,H.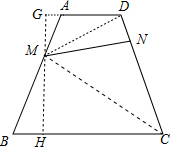
设AD=x,则BC=2x,设GH=5h,则MH=3h,MG=2h
∴S梯形ABCD=$\frac{1}{2}$(x+2x)×5h=7.5xh
S△AMD=$\frac{1}{2}$AD×MG=$\frac{1}{2}$x•2h=xh,
S△MBC=$\frac{1}{2}$BC×MH=$\frac{1}{2}$×2x•3h=3xh,
①当S四边形AMND:S四边形BCNM=1:3时,
∵S△AMD:S△MBC=xh:3xh=1:3,
∴S△MDN:S△MCN=1:3,
∵S△MDN和S△MCN高相等,
∴$\frac{DN}{CN}$=$\frac{1}{3}$,即$\frac{CN}{ND}$=3;
②当S四边形AMND:S四边形BCNM=3:1时,
∴S四边形AMND=7.5xh×$\frac{3}{4}$=$\frac{45xh}{8}$,
S四边形BCNM=7.5xh×$\frac{1}{4}$=$\frac{15xh}{8}$<S△MBC,因此不合题意.
综上所述$\frac{CN}{ND}$=3.
点评 本题主要考查了面积与等积变换,涉及相似三角形的判定与性质,等高三角形的面积比等知识,解题的关键是正确作出辅助线.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 先画图,再回答问题
先画图,再回答问题查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{x}$+$\frac{1}{3}$=$\frac{3}{2x}$ | B. | $\frac{3}{x}$+20=$\frac{3}{2x}$ | C. | $\frac{3}{x}$-$\frac{1}{3}$=$\frac{3}{2x}$ | D. | $\frac{3}{x}$-20=$\frac{3}{2x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com