
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,BC=AC=4,∠C=90°,在平面内,△ABC绕点A逆时针旋转α,对应得△AB′C′,以B′C′为直径的圆第一次与直线AB相切时.若B′C′中点为O,过O作OH⊥AB交AB′于点G,则S△B′OG=$\frac{8}{7}$.
如图,在△ABC中,BC=AC=4,∠C=90°,在平面内,△ABC绕点A逆时针旋转α,对应得△AB′C′,以B′C′为直径的圆第一次与直线AB相切时.若B′C′中点为O,过O作OH⊥AB交AB′于点G,则S△B′OG=$\frac{8}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
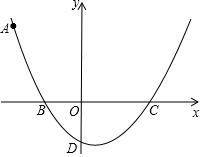 如图,在平面直角坐标系内,点O为坐标原点,经过点A(-4,4)的抛物线y=$\frac{1}{k}$(x+2)(x+a)交x轴负半轴于点B,交x轴正半轴于点C,交y轴于点D(0,-2).
如图,在平面直角坐标系内,点O为坐标原点,经过点A(-4,4)的抛物线y=$\frac{1}{k}$(x+2)(x+a)交x轴负半轴于点B,交x轴正半轴于点C,交y轴于点D(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
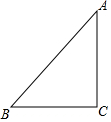 如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B.
如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
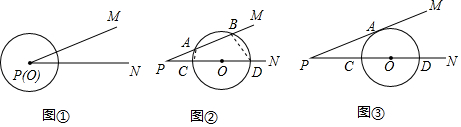
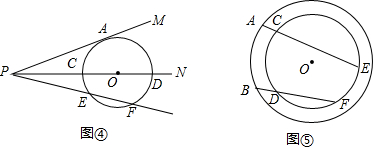
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
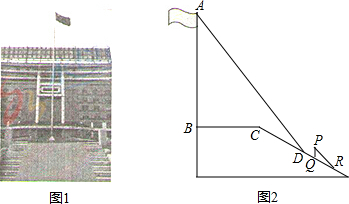
 我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)
我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com