
 如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )
如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )| A. | 3$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 5$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
分析 首先过点O作OD⊥BC于D,由垂径定理可得BC=2BD,又由圆周角定理,可求得∠BOC的度数,然后根据等腰三角形的性质,求得∠OBC的度数,利用余弦函数,即可求得答案.
解答 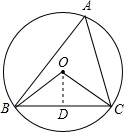 解:过点O作OD⊥BC于D,
解:过点O作OD⊥BC于D,
则BC=2BD,
∵△ABC内接于⊙O,∠BAC与∠BOC互补,
∴∠BOC=2∠A,∠BOC+∠A=180°,
∴∠BOC=120°,
∵OB=OC,
∴∠OBC=∠OCB=$\frac{1}{2}$(180°-∠BOC)=30°,
∵⊙O的半径为4,
∴BD=OB•cos∠OBC=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴BC=4$\sqrt{3}$.
故选:B.
点评 此题考查了圆周角定理、垂径定理、等腰三角形的性质以及三角函数等知识.注意掌握辅助线的作法,注意数形结合思想的应用.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 家庭人数 | 2 | 3 | 4 | 5 |
| 用气量 | 14 | 19 | 21 | 26 |
| 家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
| 用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 15 | 17 | 17 | 18 | 18 | 18 | 18 | 20 | 22 |
| 家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
| 用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 19 | 20 | 20 | 22 | 26 | 31 | 28 | 31 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
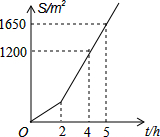 明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )| A. | 300m2 | B. | 150m2 | C. | 330m2 | D. | 450m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com