
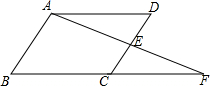
 如图,在?ABCD中,CE=$\frac{1}{2}$ED,AE,BC的延长线交于点F.若△ECF的面积为1.求四边形ABCE的面积.
如图,在?ABCD中,CE=$\frac{1}{2}$ED,AE,BC的延长线交于点F.若△ECF的面积为1.求四边形ABCE的面积. 分析 根据平行四边形的性质得到AB∥CD,AB=CD,由CE=$\frac{1}{2}$ED,得到CE=$\frac{1}{3}$AB,通过△ECF∽△ABF,根据相似三角形的性质得到$\frac{{S}_{△ECF}}{{S}_{△ABF}}$=($\frac{CE}{AB}$)2=$\frac{1}{9}$,求得S△ABF=9,即可得到结论.
解答 解:在?ABCD中,
∵AB∥CD,AB=CD,
∵CE=$\frac{1}{2}$ED,
∴CE=$\frac{1}{3}$AB,
∵AB∥CE,
∴△ECF∽△ABF,
∴$\frac{{S}_{△ECF}}{{S}_{△ABF}}$=($\frac{CE}{AB}$)2=$\frac{1}{9}$,
∵△ECF的面积为1,
∴S△ABF=9,
∴S四边形ABCE=8.
点评 本题综合考查了相似三角形的判定与性质、平行四边形的性质;解得此题的关键是根据平行四边形的性质,从而求得△ABF与△CEF的相似比.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | a>-a>$\frac{1}{a}$ | B. | a>$\frac{1}{a}$>-a | C. | $\frac{1}{a}$>-a>a | D. | -a>a>$\frac{1}{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠C=90°,CA=CB=2,分别以A,B,C为圆心,以1为半径画弧,三条弧与AB所围成的阴影部分的面积是2-$\frac{π}{2}$.
如图,在Rt△ABC中,∠C=90°,CA=CB=2,分别以A,B,C为圆心,以1为半径画弧,三条弧与AB所围成的阴影部分的面积是2-$\frac{π}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 观察函数y=2x-5的图象,回答下列问题:
观察函数y=2x-5的图象,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com