
【题目】如图,在平面在角坐标系中,抛物线y=x2-2x-3与x轴交与点A,B(点A在点B的左侧)交y轴于点C,点D为抛物线的顶点,对称轴与x轴交于点E.
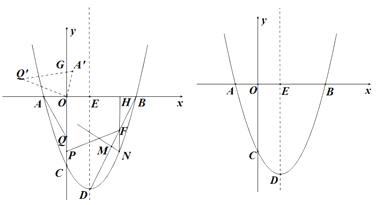
(1)连结BD,点M是线段BD上一动点(点M不与端点B,D重合),过点M作MN⊥BD交抛物线于点N(点N在对称轴的右侧),过点N作NH⊥x轴,垂足为H,交BD于点F,点P是线段OC上一动点,当MN取得最大值时,求HF+FP+![]() PC的最小值;
PC的最小值;
(2)在(1)中,当MN取得最大值HF+FP+1/3PC取得小值时,把点P向上平移个![]() 单位得到点Q,连结AQ,把△AOQ绕点O瓶时针旋转一定的角度
单位得到点Q,连结AQ,把△AOQ绕点O瓶时针旋转一定的角度![]() (0°<
(0°<![]() <360°),得到△AOQ,其中边AQ交坐标轴于点C在旋转过程中,是否存在一点G使得
<360°),得到△AOQ,其中边AQ交坐标轴于点C在旋转过程中,是否存在一点G使得![]() ?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.
?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,Q的坐标(
;(2)存在,Q的坐标(![]() ,﹣
,﹣![]() ),(
),(![]() ,
,![]() ),(﹣
),(﹣![]() ,
,![]() ),(
),(![]() ,﹣
,﹣![]() )
)
【解析】
(1)先确定点F的位置,可设点N(m,m2-2m-3),则点F(m,2m-6),可得|NF|=(2m-6)-(m2-2m-3)=-m2+4m-3,根据二次函数的性质得m=![]() 时,NF取到最大值,此时HF=2, F(2,-2),在x轴上找一点K(
时,NF取到最大值,此时HF=2, F(2,-2),在x轴上找一点K(![]() ,0),连接CK,过点F作CK的垂线交CK于点J,交y轴于点P,
,0),连接CK,过点F作CK的垂线交CK于点J,交y轴于点P,![]() ,直线KC的解析式为:
,直线KC的解析式为:![]() ,从而得到直线FJ 的解析式为:
,从而得到直线FJ 的解析式为:![]() 联立解出点J(
联立解出点J(![]() ,
, ![]()
)得FP+![]() PC的最小值即为FJ的长,且
PC的最小值即为FJ的长,且![]() , 最后得出
, 最后得出![]() ;(2)由题意可得出点Q(0,-2),A2=
;(2)由题意可得出点Q(0,-2),A2=![]() ,应用“直角三角形斜边上的中线等于斜边上的一半”取AQ的中点G,连接OG,则OG=GQ=
,应用“直角三角形斜边上的中线等于斜边上的一半”取AQ的中点G,连接OG,则OG=GQ=![]() AQ=
AQ=![]() ,此时,∠AQ0=∠GOQ,把△AOQ绕点O顺时针旋转一定的角度
,此时,∠AQ0=∠GOQ,把△AOQ绕点O顺时针旋转一定的角度![]() (0°<
(0°<![]() <360°),得到△A'OQ',其中边A’Q’交坐标轴于点G,则用0G=GQ’,分四种情况求解即可.
<360°),得到△A'OQ',其中边A’Q’交坐标轴于点G,则用0G=GQ’,分四种情况求解即可.
解:(1)如图1

∵抛物线y=x2﹣2x﹣3与x轴交于点A,B(点A在点B的左侧),交y轴于点C
∴令y=0解得:x1=﹣1,x2=3,令x=0,解得:y=﹣3,
∴A(﹣1,0),B(3,0),C(0,﹣3)
∵点D为抛物线的顶点,且![]() ﹣4
﹣4
∴点D的坐标为D(1,﹣4)
∴直线BD的解析式为:y=2x﹣6,
由题意,可设点N(m,m2﹣2m﹣3),则点F(m,2m﹣6)
∴|NF|=(2m﹣6)﹣(m2﹣2m﹣3)=﹣m2+4m﹣3
∴当m=![]() =2时,NF 取到最大值,此时MN取到最大值,此时HF=2,
=2时,NF 取到最大值,此时MN取到最大值,此时HF=2,
此时,N(2,﹣3),F(2,﹣2),H(2,0)
在x轴上找一点K(![]() ,0),连接CK,过点F作CK的垂线交CK于点J点,交y轴于点P,
,0),连接CK,过点F作CK的垂线交CK于点J点,交y轴于点P,
∴sin∠OCK=![]() ,直线KC的解析式为:
,直线KC的解析式为:![]() ,且点F(2,﹣2),
,且点F(2,﹣2),
∴PJ=![]() PC,直线FJ的解析式为:
PC,直线FJ的解析式为:![]()
∴点J(![]() ,
, ![]() )
)
∴FP+![]() PC的最小值即为FJ的长,且
PC的最小值即为FJ的长,且![]()
∴![]() ;
;
(2)由(1)知,点P(0, ![]() ),
),
∵把点P向上平移![]() 个单位得到点Q
个单位得到点Q
∴点Q(0,﹣2)
∴在Rt△AOQ中,∠AOG=90°,AQ=![]() ,取AQ的中点G,连接OG,则OG=GQ=
,取AQ的中点G,连接OG,则OG=GQ=![]() AQ=
AQ=![]() ,此时,∠AQO=∠GOQ
,此时,∠AQO=∠GOQ
把△AOQ绕点O顺时针旋转一定的角度α(0°<α<360°),得到△A′OQ′,其中边A′Q′交坐标轴于点G
①如图2

G点落在y轴的负半轴,则G(0,﹣![]() ),过点Q'作Q'I⊥x轴交x轴于点I,且∠GOQ'=∠Q'
),过点Q'作Q'I⊥x轴交x轴于点I,且∠GOQ'=∠Q'
则∠IOQ'=∠OA'Q'=∠OAQ,
∵sin∠OAQ=![]() =
=![]() =
=![]()
∴![]() ,解得:|IO|=
,解得:|IO|=![]()
∴在Rt△OIQ'中根据勾股定理可得|OI|=![]()
∴点Q'的坐标为Q'(![]() ,﹣
,﹣![]() );
);
②如图3,![]()

当G点落在x轴的正半轴上时,同理可得Q'(![]() ,
,![]() )
)
③如图4

当G点落在y轴的正半轴上时,同理可得Q'(﹣![]() ,
,![]() )
)
④如图5
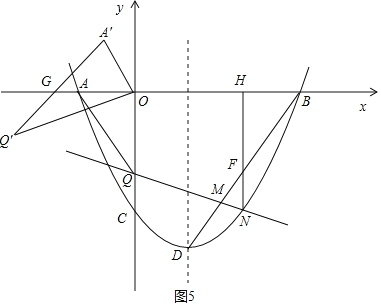
当G点落在x轴的负半轴上时,同理可得Q'(﹣![]() ,﹣
,﹣![]() )
)
综上所述,所有满足条件的点Q′的坐标为:(![]() ,﹣
,﹣![]() ),(
),(![]() ,
,![]() ),(﹣
),(﹣![]() ,
,![]() ),(
),(![]() ,﹣
,﹣![]() )
)


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
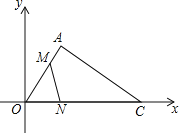
【题目】如图,点O是平面直角坐标系的原点,点A(![]() ,3),AC⊥OA与x轴的交点为C.动点M以每秒
,3),AC⊥OA与x轴的交点为C.动点M以每秒![]() 个单位长度由点A向点O运动.同时,动点N以每秒3个单位长度由点O向点C运动,当一动点先到终点时,另一动点立即停止运动.
个单位长度由点A向点O运动.同时,动点N以每秒3个单位长度由点O向点C运动,当一动点先到终点时,另一动点立即停止运动.
(1)写出∠AOC的值;
(2)用t表示出四边形AMNC的面积;
(3)求点P的坐标,使得以O、N、M、P为顶点的四边形是特殊的平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
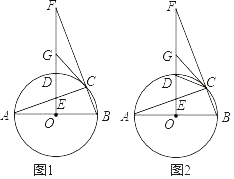
【题目】如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG
(1)判断CG与⊙O的位置关系,并说明理由;
(2)求证:2OB2=BCBF;
(3)如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,已知抛物线![]() 的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.

(1)直接写出D点和E点的坐标;
(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,![]() =5:6?
=5:6?
(3)图2所示的抛物线是由![]() 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在精准扶贫的过程中,某驻村服务队结合当地高山地形,决定在该村种植中药材川香、贝母、黄连增加经济收人,经过一段时间,该村已种植的川香、贝母、黄连面积之比4:3:5,是根据中药材市场对川香、贝母、黄连的需求量,将在该村余下土地上继续种植这三种中药材,经测算需将余下土地面积的![]() 种植黄连,则黄连种植总面积将达到这三种中药材种植总面积的
种植黄连,则黄连种植总面积将达到这三种中药材种植总面积的![]() .为使川香种植总面积与贝母种植总面积之比达到3:4,则该村还需种植贝母的面积与该村种植这三种中药材的总面积之比是____.
.为使川香种植总面积与贝母种植总面积之比达到3:4,则该村还需种植贝母的面积与该村种植这三种中药材的总面积之比是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代第一部数学专著《九章算术》中有这样一道题:今有上禾7束,减去其中之实1斗,加下禾2束,则得实10斗.下禾8束,加实1斗和上禾2束,则得实10斗,问上禾、下禾1束得实多少?
译文为:今有上等禾7捆结出的粮食,减去1斗再加上2捆下等禾结出的粮食,共10斗;下等禾8捆结出的粮食,加上1斗和上等禾2捆结出的粮食,共10斗,问上等禾和下等禾1捆各能结出多少斗粮食?(斗为体积单位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=5,BC=8,若△ABC沿射线BC方向平移m个单位得到△DEF,顶点A,B,C分别与D,E,F对应,若以点A,D,E为顶点的三角形是等腰三角形,则m的值是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com