
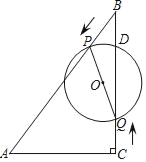
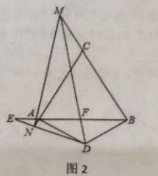
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=6cmЃЌЁЯABC=30ЁуЃЌЖЏЕуPДгЕуBГіЗЂЃЌдкBAБпЩЯвдУПУы2cmЕФЫйЖШЯђЕуAдШЫйдЫЖЏЃЌЭЌЪБЖЏЕуQДгЕуCГіЗЂЃЌдкCBБпЩЯвдУПУы![]() cmЕФЫйЖШЯђЕуBдШЫйдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЈ0ЁмtЁм6ЃЉЃЌСЌНгPQЃЌвдPQЮЊжБОЖзїЁбOЃЎ
cmЕФЫйЖШЯђЕуBдШЫйдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЈ0ЁмtЁм6ЃЉЃЌСЌНгPQЃЌвдPQЮЊжБОЖзїЁбOЃЎ
ЃЈ1ЃЉЕБt=1ЪБЃЌЧѓЁїBPQЕФУцЛ§ЃЛ
ЃЈ2ЃЉЩшЁбOЕФУцЛ§ЮЊyЃЌЧѓyгыtЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉШєЁбOгыRtЁїABCЕФвЛЬѕБпЯрЧаЃЌЧѓtЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЕБt=1ЪБЃЌSЁїBPQ=![]() ЃЛЃЈ2ЃЉy=
ЃЛЃЈ2ЃЉy=![]() t2Љ18Іаt+27ІаЃЛЃЈ3ЃЉШєЁбOгыRtЁїABCЕФвЛЬѕБпЯрЧаЃЌtЕФжЕЮЊ3Лђ
t2Љ18Іаt+27ІаЃЛЃЈ3ЃЉШєЁбOгыRtЁїABCЕФвЛЬѕБпЯрЧаЃЌtЕФжЕЮЊ3Лђ![]() Лђ0Лђ
Лђ0Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉСЌНгDPЃЌИљОнЁїBPMЁзЁїBACЃЌПЩЕУPD=tЃЌBQ=![]() ЃЈ6-tЃЉЃЌШЛКѓЕУЕНSЁїBPQ=
ЃЈ6-tЃЉЃЌШЛКѓЕУЕНSЁїBPQ=![]() BQPDМДПЩЕУГіНсТлЃЛ
BQPDМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЯШБэЪОГіDPЃЌBDЃЌНјЖјРћгУЙДЙЩЖЈРэЧѓГіPQЕФЦНЗНЃЌзюКѓгУдВЕФУцЛ§ЙЋЪНМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЗжЕБЁбOгыBCЯрЧаЁЂЁбOгыABЯрЧаЃЌЁбOгыACЯрЧаЪБЃЌШ§жжЧщПіЗжРрЬжТлМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌ
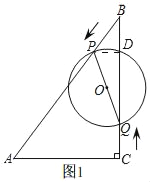
дкRtЁїABCжаЃЌЁЯABC=30ЁуЃЌAC=6ЃЌ
ЁрAB=12ЃЌBC=6![]() ЃЌ
ЃЌ
гЩдЫЖЏжЊЃЌBP=2tЃЌCQ=![]() tЃЌ
tЃЌ
ЁрBQ=BCЉCQ=![]() ЃЈ6ЉtЃЉЃЌ
ЃЈ6ЉtЃЉЃЌ
СЌНгDPЃЌ
ЁпPQЪЧЁбOЕФжБОЖЃЌ
ЁрЁЯPDQ=90Ёу
ЁпЁЯC=90ЁуЃЌ
ЁрPDЁЮACЃЎ
ЁрЁїBPDЁзЁїBACЃЌ
Ёр![]()
Ёр![]() ЃЌ
ЃЌ
ЁрDP=tЃЌBD=![]() tЃЌ
tЃЌ
SЁїBPQ=![]() BQPD=
BQPD=![]() ЁС
ЁС![]() ЃЈ6ЉtЃЉt=Љ
ЃЈ6ЉtЃЉt=Љ![]() t2+3
t2+3![]() t
t
ЁрЕБt=1ЪБЃЌSЁїBPQ=Љ![]() +3
+3![]() =
=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉDQ=|BQЉBD|=![]() ЃЈ6ЉtЃЉЉ
ЃЈ6ЉtЃЉЉ![]() t|=2
t|=2![]() |3Љt|ЃЌPQ2=PD2+DQ2=t2+[2
|3Љt|ЃЌPQ2=PD2+DQ2=t2+[2![]() ЃЈ3ЉtЃЉ]2=13t2Љ72t+108ЃЌ
ЃЈ3ЉtЃЉ]2=13t2Љ72t+108ЃЌ
Ёрy=ІаЁСЃЈ![]() ЃЉ2=
ЃЉ2=![]() t2Љ18Іаt+27ІаЃЌ
t2Љ18Іаt+27ІаЃЌ
ЃЈ3ЃЉгЩдЫЖЏжЊЃЌBP=2tЃЌCQ=![]() tЃЌ
tЃЌ
ЁрBQ=BCЉCQ=![]() ЃЈ6ЉtЃЉЃЌ
ЃЈ6ЉtЃЉЃЌ
ЕБЁбOгыBCЯрЧаЪБЃЌPQЁЭBCЃЌ
ЁрЁїBPQЁзЁїBACЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрt1=3ЃЌ
ЕБЁбOгыABЯрЧаЪБЃЌPQЁЭABЃЌ
ЁрЁїBPQЁзЁїBCA
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрt2=![]() ЃЌ
ЃЌ
ЕБЁбOгыACЯрЧаЪБЃЌШчЭМ2ЃЌЙ§ЕуOзїOHЁЭACгкЕуHЃЌНЛPDгкЕуNЃЌ
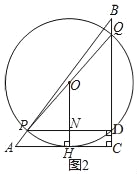
ЁрOHЁЮBCЃЌ
ЁпЕуOЪЧPQЕФжаЕуЃЌ
ЁрON=![]() QDЃЌ
QDЃЌ
гЩЃЈ1ЃЉжЊЃЌBQ=![]() ЃЈ6ЉtЃЉЃЌBD=
ЃЈ6ЉtЃЉЃЌBD=![]() tЃЌ
tЃЌ
ЁрQD=BDЉBQ=2![]() ЃЈtЉ3ЃЉЃЌDC=BCЉBD=6
ЃЈtЉ3ЃЉЃЌDC=BCЉBD=6![]() Љ
Љ![]() t=
t=![]() ЃЈ6ЉtЃЉ
ЃЈ6ЉtЃЉ
ЁрOH=ON+NH=![]() QD+DC=
QD+DC=![]() ЁС2
ЁС2![]() ЃЈtЉ3ЃЉ+
ЃЈtЉ3ЃЉ+![]() ЃЈ6ЉtЃЉ=3
ЃЈ6ЉtЃЉ=3![]() ЃЌ
ЃЌ
ЁрPQ=2OH=6![]() ЃЌ
ЃЌ
гЩЃЈ2ЃЉжЊЃЌPQ2=13t2Љ72t+108
Ёр13t2Љ72t+108=36ЁС3
НтЕУt3=0ЃЌt4=![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌШєЁбOгыRtЁїABCЕФвЛЬѕБпЯрЧаЃЌtЕФжЕЮЊ3Лђ![]() Лђ0Лђ
Лђ0Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
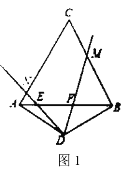
ЁОЬтФПЁПЫФБпаЮ![]() ЪЧгЩЕШБп
ЪЧгЩЕШБп![]() КЭЖЅНЧЮЊ120ЁуЕФЕШбќШ§НЧаЮ
КЭЖЅНЧЮЊ120ЁуЕФЕШбќШ§НЧаЮ![]() ЦДГЩЃЌНЋвЛИі60ЁуНЧЖЅЕуЗХдкЕу
ЦДГЩЃЌНЋвЛИі60ЁуНЧЖЅЕуЗХдкЕу![]() ДІЃЌ60ЁуНЧСНБпЗжБ№НЛжБЯп
ДІЃЌ60ЁуНЧСНБпЗжБ№НЛжБЯп![]() гк
гк![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гк
гк![]() СНЕуЃЎ
СНЕуЃЎ
ЃЈ1ЃЉЕБ![]() ЖМдкЯпЖЮ
ЖМдкЯпЖЮ![]() ЩЯЪБЃЌЬНОП
ЩЯЪБЃЌЬНОП![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
жЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ2ЃЉЕБ![]() дкБп
дкБп![]() ЕФбгГЄЯпЩЯЪБЃЌЧѓжЄЃК
ЕФбгГЄЯпЩЯЪБЃЌЧѓжЄЃК![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌBAЃНBCЃЌCDКЭBEЪЧЁїABCЕФСНЬѕИпЃЌЁЯBCDЃН45ЁуЃЌBEгыCDНЛгкЕуHЃЎ

ЃЈ1ЃЉЧѓжЄЃКЁїBDHЁеЁїCDAЃЛ
ЃЈ2ЃЉЧѓжЄЃКBHЃН2AEЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋОиаЮABCDбиBDЖделЃЌЕуAТфдкEДІЃЌBEгыCDЯрНЛгкFЃЌШєAD=3ЃЌBD=6ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїEDFЁеЁїCBFЃЛ
ЃЈ2ЃЉЧѓЁЯEBCЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
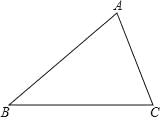
ЁОЬтФПЁПШчЭМЃЌШёНЧЁїABC жа BCЃНaЃЌACЃНbЃЌABЃНcЃЌМЧШ§НЧаЮ ABC ЕФУцЛ§ЮЊ SЃЎ
(1)ЧѓжЄЃКSЃН![]() absinC;
absinC;
(2)ЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
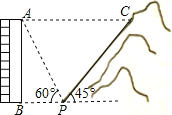
ЁОЬтФПЁПШчЭМЃЌвЛОгУёТЅЕзВПBгыЩННХPЮЛгкЭЌвЛЫЎЦНЯпЩЯЃЌаЁРюдкPДІВтЕУОгУёТЅЖЅAЕФбіНЧЮЊ60ЁуЃЌШЛКѓЫћДгPДІбиЦТНЧЮЊ45ЁуЕФЩНЦТЯђЩЯзпЕНCДІЃЌетЪБЃЌPC=30 mЃЌЕуCгыЕуAЧЁКУдкЭЌвЛЫЎЦНЯпЩЯЃЌЕуAЁЂBЁЂPЁЂCдкЭЌвЛЦНУцФкЁЃ
ЃЈ1ЃЉЧѓОгУёТЅABЕФИпЖШЃЛ
ЃЈ2ЃЉЧѓCЁЂAжЎМфЕФОрРыЁЃЃЈОЋШЗЕН0.1mЃЌВЮПМЪ§ОнЃК ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИпжаеаЩњжИБъЕНаЃЪЧЮвЪажаПМеаЩњжЦЖШИФИяЕФвЛЯюживЊДыЪЉЃЎФГГѕМЖжабЇЖдИУаЃНќЫФФъжИБъЕНаЃБЃЫЭЩњШЫЪ§НјааСЫЭГМЦЃЌжЦГЩСЫШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃК
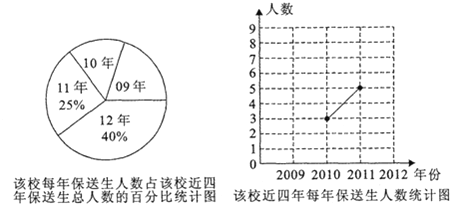
ЃЈ1ЃЉИУаЃНќЫФФъБЃЫЭЩњШЫЪ§ЕФМЋВюЪЧ ЃЎЧыНЋелЯпЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉИУаЃ2009ФъжИБъЕНаЃБЃЫЭЩњжажЛга1ЮЛХЎЭЌбЇЃЌбЇаЃДђЫуДгжаЫцЛњбЁГі2ЮЛЭЌбЇСЫНтЫћУЧНјШЫИпжаНзЖЮЕФбЇЯАЧщПіЃЎЧыгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓГіЫљбЁСНЮЛЭЌбЇЧЁКУЪЧ1ЮЛФаЭЌбЇКЭ1ЮЛХЎЭЌбЇЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃОХФъМЖ10ИіАрЪІЩњОйааБЯвЕЮФвеЛубнЃЌУПАр2ИіНкФПЃЌгаИшГЊгыЮшЕИСНРрНкФПЃЌФъМЖЭГМЦКѓЗЂЯжИшГЊРрНкФПЪ§БШЮшЕИРрНкФПЪ§ЕФ2БЖЩй4Иі.
ЃЈ1ЃЉОХФъМЖЪІЩњБэбнЕФИшГЊгыЮшЕИРрНкФПЪ§ИїгаЖрЩйИіЃП
ЃЈ2ЃЉИУаЃЦпЁЂАЫФъМЖЪІЩњгааЁЦЗНкФПВЮгыЃЌдкИшГЊЁЂЮшЕИЁЂаЁЦЗШ§РрНкФПжаЃЌУПИіНкФПЕФбнГіЦНОљгУЪБЗжБ№ЪЧ5ЗжжгЁЂ6ЗжжгЁЂ8ЗжжгЃЌдЄМЦЫљгабнГіНкФПНЛНггУЪБЙВЛЈ15Зжжг.ШєДг20ЃК00ПЊЪМЃЌ22ЃК30жЎЧАбнГіНсЪјЃЌЮЪВЮгыЕФаЁЦЗРрНкФПзюЖрФмгаЖрЩйИіЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCгыЁїA1B1C1ЪЧЮЛЫЦЭМаЮЃЎдкЭјИёЩЯНЈСЂЦНУцжБНЧзјБъЯЕЃЌЪЙЕУЕуAЕФзјБъЮЊЃЈ1ЃЌЉ6ЃЉЃЎ
ЃЈ1ЃЉдкЭМЩЯБъГіЕуЃЌЁїABCгыЁїA1B1C1ЕФЮЛЫЦжааФPЃЎВЂаДГіЕуPЕФзјБъЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉвдЕуAЮЊЮЛЫЦжааФЃЌдкЭјИёЭМжазїЁїAB2C2ЃЌЪЙЁїAB2C2КЭЁїABCЮЛЫЦЃЌЧвЮЛЫЦБШЮЊ1ЃК2ЃЌВЂаДГіЕуC2ЕФзјБъЮЊЁЁ ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com