
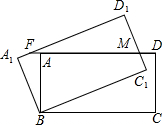
 如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=$\sqrt{3}$,则AF的长度为=2-$\sqrt{3}$.
如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=$\sqrt{3}$,则AF的长度为=2-$\sqrt{3}$. 分析 延长BA交A1D1于H,先确定出∠AFD1=30°,用含30°的直角三角形的性质依次求出BH,AF即可.
解答 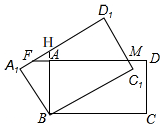 解:如图,延长BA交A1D1于H,
解:如图,延长BA交A1D1于H,
由旋转得,A1B=AB=1,∠CBC1=∠ABA1=30°,∠BA1D1=∠BAF=90°,
在四边形A1BAF中,根据四边形的内角和得,∠A1FA=150°,
∴∠AFH∠=30°,
在Rt△A1BH中,A1B=1,∠A1BA=30°,
∴BH=$\frac{2}{3}\sqrt{3}$,
∴AH=BH-AB=$\frac{2}{3}\sqrt{3}$-1,
在Rt△AFH中,∠AFH=30°,
∴AF=$\sqrt{3}$AH=2-$\sqrt{3}$,
故答案为:2-$\sqrt{3}$.
点评 本题考查了旋转的性质、矩形的性质、以及含30°角的直角三角形的性质的应用;熟练掌握旋转的性质和矩形的性质,并能进行推理计算是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
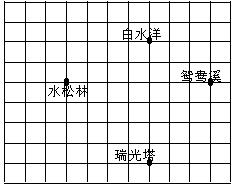 暑假时小明和小颖到福建屏南旅游,小明在如上图所示的旅游简图上建立了直角坐标系,但他只告诉小颖白水洋的坐标是(2,5),请你帮小颖写出鸳鸯溪的坐标是(5,3).
暑假时小明和小颖到福建屏南旅游,小明在如上图所示的旅游简图上建立了直角坐标系,但他只告诉小颖白水洋的坐标是(2,5),请你帮小颖写出鸳鸯溪的坐标是(5,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x>3\\ x<1\end{array}\right.$ | B. | $\left\{\begin{array}{l}3x<5\\ 2x-1<9\end{array}\right.$ | C. | $\left\{\begin{array}{l}x-1>3\\ y+2<1\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-1>3\\ x-3<2\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为2,点E是BC边上的一动点,点F是CD上一点,且CE=DF,AF、DE相交于点O,BO=BA,则OC的值为$\frac{2}{5}$$\sqrt{10}$.
如图,正方形ABCD的边长为2,点E是BC边上的一动点,点F是CD上一点,且CE=DF,AF、DE相交于点O,BO=BA,则OC的值为$\frac{2}{5}$$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com