Question

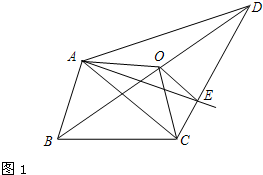
我们把能平分四边形面积的直线称为“好线”.利用下面的作图，可以得到四边形的“好线”：如图1，在四边形ABCD中，取对角线BD的中点O，连结OA、OC. 显然，折线AOC能平分四边形ABCD的面积，再过点O作OE∥AC交CD于E，则直线AE即为一条“好线”.

（1）试说明直线AE是“好线”的理由；

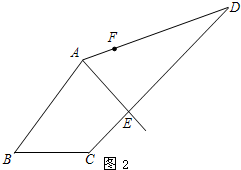
（2）如图2，AE为一条“好线”，F为AD边上的一点，请作出经过F点的“好线”，只需对画图步骤作适当说明（不需要说明“好线”的理由）.

 

Answer 1

【答案】

（1）∵AO是△ABD的中线，∴AO平分△ABD的面积，

同理，CO平分△CBD的面积，于是，折线AOC平分四边形ABCD的面积.

        若记四边形ABCD的面积为S，有S_{四边形OABC}＝S.

        ∵OE∥AC，∴S_△OAC＝S_△EAC……………………………………………… (1分)

        ∴S_{四边形EABC}＝S_△EAC＋S_△ABC＝S_△OAC＋S_△ABC＝S_{四边形OABC}＝S……………(2分)

       ∴直线AE是四边形ABCD的一条好线. ……………………………………(3分)

     （2）连结EF，过点A作EF的平行线，交CD于点P，作直线PF，

          则直线PF即为所要求作的好线.……………………………………(5分)

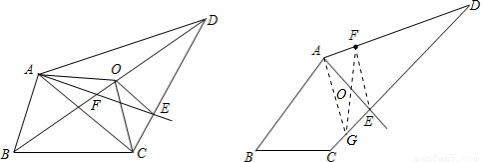
【解析】（1）设AE与OC的交点是F．要说明直线AE是“好线”，根据已知条件中的折线AOC能平分四边形ABCD的面积，只需说明三角形AOF的面积等于三角形CEF的面积．则根据两条平行线间的距离相等，结合三角形的面积个数可以证明三角形AOE的面积等于三角形COE的面积，再根据等式的性质即可证明；

（2）根据两条平行线间的距离相等，只需借助平行线即可作出过点F的“好线”．