练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

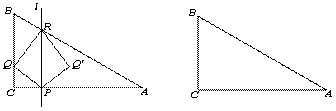
    如图，△ABC中，∠C＝90°，AC=8cm，BC=6cm，点P、Q同时从点C出发，以1cm/s的速度分别沿CA、CB匀速运动，当点Q到达点B时，点P、Q同时停止运动．过点P作AC的垂线l交AB于点R，连接PQ、RQ，并作△PQR关于直线l对称的图形，得到△PQ'R．设点Q的运动时间为t（s），△PQ'R与△PAR重叠部分的面积为S（cm2）．

    （1）t为何值时，点Q' 恰好落在AB上？

    （2）求S与t的函数关系式，并写出t的取值范围．

    （3）S能否为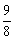？若能，求出此时t的值；若不能，请说明理由．

     


     


    （1）当t=时，点Q' 恰好落在AB上.

    （2）当0＜t≤时，；当＜t≤6时，   

    （3）由（2）问可得，当0＜t≤时， ；

    当＜t≤6时，；

    解得，或，此时.             


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


     如图4所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是（　　）

    A．∠3=∠4   B．∠A=∠DCEC． ∠D=∠DCE  D．∠D+∠ACD=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ）如图，折叠长方形的一边，使点 落在边上的点处， ，，求：（1）的长；（2）的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知，在二次函数的图象上，若，则（填“>”、“=”或“<”）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某德阳特产专卖店销售“中江柚”，已知“中江柚”的进价为每个10元，现在的售价是每个16元，每天可卖出120个．市场调查反映：如调整价格，每涨价1元，每天要少卖出10个；每降价1元，每天可多卖出30个．

    （1）如果专卖店每天要想获得770元的利润，且要尽可能的让利给顾客，那么售价应涨价多少元？

    （2）请你帮专卖店老板算一算，如何定价才能使利润最大，并求出此时的最大利润？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


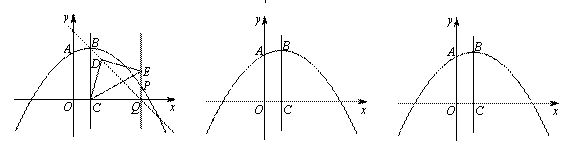
    抛物线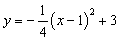与y轴交于点A，顶点为B，对称轴BC与x轴交于点C．点P在抛物线上，直线PQ//BC交x轴于点Q，连接BQ．

    （1）若含45°角的直角三角板如图所示放置，其中一个顶点与点C重合，直角顶点D在BQ上，另一个顶点E在PQ上，求直线BQ的函数解析式；

    （2）若含30°角的直角三角板的一个顶点与点C重合，直角顶点D在直线BQ上（点D不与点Q重合），另一个顶点E在PQ上，求点P的坐标．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知，抛物线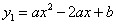经过A(-1，0)，C(2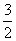，)两点，

    与x轴交于另一点B．

    （1）求此抛物线的解析式；

    （2）若抛物线的顶点为M，点P为线段OB上一动点 （不与点B重合），点Q在线段MB上移动，且∠MPQ=45°，设线段OP=x，MQ=，求y2与x的函数关系式，

    并直接写出自变量x的取值范围．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    关于二次函数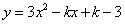，以下结论：① 抛物线交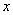轴有两个不同的交点；②不论k取何值，抛物线总是经过一个定点；③设抛物线交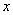轴于A、B两点，若AB=1，则k=9；；④ 抛物线的顶点在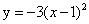图像上．其中正确的序号是（    ）

    A．①②③④　      B．②③ 　     C．②④　     D．①②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一次函数，若随的增大而增大，则的值可以是（    ）

    （A）1       （B）2      （C）3      （D）4

    查看答案和解析>>

    同步练习册答案