
 如图,E为?ABCD的边AB延长线上的一点,且BE:AB=2:3,连接DE交BC于点F,则CF:AD=3:5.
如图,E为?ABCD的边AB延长线上的一点,且BE:AB=2:3,连接DE交BC于点F,则CF:AD=3:5. 分析 先证明△CDF∽△BEF,所以$\frac{CD}{BE}=\frac{CF}{BF}$,由平行四边形的性质可知,$\frac{CD}{BE}=\frac{AB}{BE}=\frac{3}{2}$,从而可知$\frac{CF}{CB}=\frac{CF}{AD}$=$\frac{3}{5}$.
解答 解:由题意可知:CD∥AE,CD=AB
∴△CDF∽△BEF
∴$\frac{CD}{BE}=\frac{CF}{BF}$
∵$\frac{CD}{BE}=\frac{AB}{BE}=\frac{3}{2}$
∴$\frac{CF}{BF}=\frac{3}{2}$,
∴$\frac{CF}{CB}=\frac{3}{5}$,
∵AD=BC,
∴$\frac{CF}{CB}=\frac{CF}{AD}$=$\frac{3}{5}$,
故答案为:3:5
点评 本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于中等题型.


科目:初中数学 来源: 题型:选择题
| A. | 随意掷一枚均匀的硬币两次,至少有一次反面朝上 | |
| B. | 今年冬天黑龙江会下雪 | |
| C. | 随意掷一枚均匀的正方体骰子两次,两次朝上面的点数之和为1 | |
| D. | 一个转盘被分成6个扇形,按红、白、白、红、红、白排列,转动转盘,指针停在红色区域 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
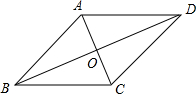 如图,在四边形ABCD中,AB∥DC,对角线AC与BD相交于点O,AO=CO.请你再添一个条件,就能推出四边形ABCD是菱形,则下列条件不符合的是( )
如图,在四边形ABCD中,AB∥DC,对角线AC与BD相交于点O,AO=CO.请你再添一个条件,就能推出四边形ABCD是菱形,则下列条件不符合的是( )| A. | BD平分∠ABC | B. | AB=AD | C. | AC⊥BD | D. | OB=OA |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
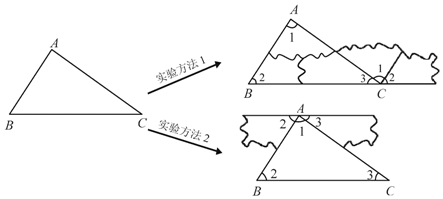
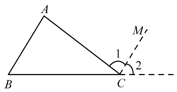
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
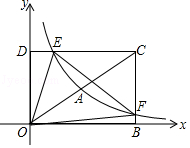 如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A(3,2),交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A(3,2),交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com