
【题目】如图,过点P作PA,PB,分别与以OA为半径的半圆切于A,B,延长AO交切线PB于点C,交半圆与于点D.
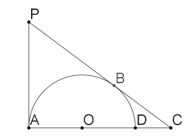
(1)若PC=5,AC=4,求BC的长;
(2)设DC:AD=1:2,求![]() 的值.
的值.
科目:初中数学 来源: 题型:
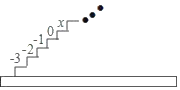
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣3,﹣2,﹣1,0,且任意相邻四个台阶上数的和都相等.
(1)求第五个台阶上的数x是多少?
(2)求前21个台阶上的数的和是多少?
(3)发现:数的排列有一定的规律,第n个﹣2出现在第 个台阶上;
(4)拓展:如果倩倩小同学一步只能上1个或者2个台阶,那么她上第一个台阶的方法有1种:1=1,上第二个台阶的方法有2种:1+1=2或2=2,上第三个台阶的方祛有3种:1+1+1=3、1+2=3或2+1=3,…,她上第五个台阶的方法可以有 种.
查看答案和解析>>
科目:初中数学 来源: 题型:
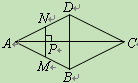
【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直
线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则
y关于x的函数图象大致形状是【 】

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在圆环形路上有均匀分布的四家工厂甲、乙、丙、丁,每家工厂都有足够的仓库供产品储存.现要将所有产品集中到一家工厂的仓库储存,已知甲、乙、丙、丁四家工厂的产量之比为1:2:3:5.若运费与路程、运的数量成正比例,为使选定的工厂仓库储存所有产品时总的运费最省,应选的工厂是( )
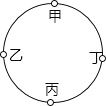
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,AC=BC,过C作CD//AB.若AD平分∠CAB,则下列说法错误的是( )
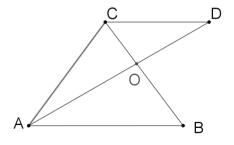
A. BC=CD
B. BO:OC=AB:BC
C. △CDO≌△BAO
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小淇、小尧对一道中考题目的部分解答.
题目:刘阿姨到超市购买大米,第一次按原价购买,用了105元.几天后,遇上这种大米8折出售,她用140元又买了一些,两次一共购买了40kg.这种大米的原价是多少?
小淇:![]() ;小尧:
;小尧:![]() .
.
根据以上信息,解答下列问题.
(1)小淇同学所列方程中的x表示 ,小尧同学所列方程中的y表示 ;
(2)在上述两个方程中任选一个求解,并回答题目中的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的函数关系图象,其中M为曲线部分的最低点下列说法错误的是( )
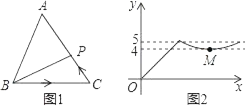
A. △ABC是等腰三角形B. AC边上的高为4
C. △ABC的周长为16D. △ABC的面积为10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC交AC于点E,AC的反向延长线交⊙O于点F.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若∠C=30°,⊙O的半径为6,求弓形AF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+5(a≠0)交直线y=kx+n(k>0)于A(1,1),B两点,交y轴于点C,直线AB交y轴于点D.已知该抛物线的对称轴为直线x=![]() .
.
(1)求a,b的值;
(2)记直线AB与抛物线的对称轴的交点为E,连接CE,CB.若△CEB的面积为![]() ,求k,n的值.
,求k,n的值.
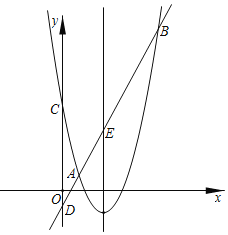
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com