
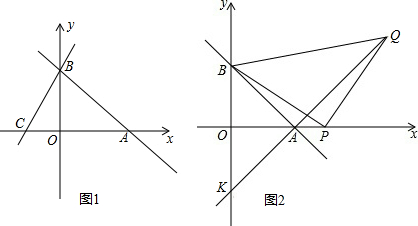
分析 (1)设BC的解析式是Y=ax+c,由直线AB:y=-x-b过A(6,0),可以求出b,因此可以求出B点的坐标,再由已知条件可求出C点的坐标,把B,C点的坐标分别代入求出a和c的值即可;
(2)不变化,过Q作QH⊥x轴于H,首先证明△BOP≌△HPQ,再分别证明△AHQ和△AOK为等腰直角三角形,问题得解;
(3)过E、F分别作EM⊥x轴,FN⊥x轴,则∠EMD=∠FND=90°,由题目的条件证明△NFD≌△EDM,进而得到FN=ME,联立直线AB:y=-x-b和y=2x-k求出交点E和F的纵坐标,再利用等底等高的三角形面积相等即可求出k的值;
解答 解:(1)直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,
∴0=-6-b,
∴b=-6,
∴直线AB的解析式为:y=-x+6.
∴B(0,6),
∴OB=6,
∵OB:OC=3:1,
∴OC=$\frac{1}{3}$OB=2,∴C(-2,0),
设BC的解析式是y=ax+c,
∴$\left\{\begin{array}{l}{6=0•a+c}\\{0=-2a+c}\end{array}\right.$
∴$\left\{\begin{array}{l}{a=3}\\{b=6}\end{array}\right.$,
∴直线BC的解析式是:y=3x+6;
(2)K点的位置不发生变化,K(0,-6).
如图1,过Q作QH⊥x轴于H,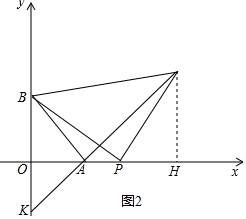
∵△BPQ是等腰直角三角形,
∴∠BPQ=90°,PB=PQ,
∵∠BOA=∠QHA=90°,
∴∠BPO=∠PQH,
在△BOP与△HPQ中,
$\left\{\begin{array}{l}{∠AOB=∠QHA}\\{∠BPO=∠PQH}\\{BP=PQ}\end{array}\right.$,
∴△BOP≌△HPQ(AAS),
∴PH=BO,OP=QH,
∴PH+PO=BO+QH,
即OA+AH=BO+QH,
又∵OA=OB,
∴AH=QH,
∴△AHQ是等腰直角三角形,
∴∠QAH=45°,
∴∠OAK=45°,
∴△AOK为等腰直角三角形,
∴OK=OA=6,
∴K(0,-6);
(3)如图2,过E、F分别作EM⊥x轴,FN⊥x轴,则∠EMD=∠FND=90°.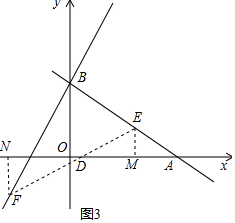
∵S△EBD=SFBD,
∴DE=DF.
又∵∠NDF=∠EDM,
在△NFD与△EDM中,
$\left\{\begin{array}{l}{∠FND=∠DEM}\\{∠NDF=∠EDM}\\{DE=DF}\end{array}\right.$,
∴△NFD≌△EDM(AAS),
∴FN=ME.
解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x-k}\\{y=-x+6}\end{array}\right.$得E点的纵坐标yE=$\frac{6-2k}{3}$,
解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x-k}\\{y=3x+6}\end{array}\right.$得F点的纵坐标yF=$\frac{-6-6k}{5}$
∵FN=-yF,ME=yE,
∴k=$\frac{3}{7}$;
当k=$\frac{3}{7}$时,存在直线EF:y=$\frac{1}{2}$x-$\frac{3}{7}$,使得S△EBD=S△FBD.
点评 此题综合考查了用待定系数法求一次函数的解析式、全等三角形的判定和全等三角形的性质,以及等腰直角三角形的判定和性质,解题的关键是正确求解析式以及借助于函数图象全面的分析问题.


科目:初中数学 来源: 题型:解答题
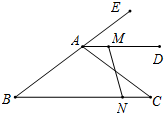 如图,在△ABC中,AB=5cm,BC=8cm,AD为△ABC的外角平分线,且AD∥BC,点M从A出发,以1cm/s的速度沿射线AD匀速运动,同时点N以相同的速度从C出发沿CB匀速向点B运动,当点N到达B时,点M也停止运动.
如图,在△ABC中,AB=5cm,BC=8cm,AD为△ABC的外角平分线,且AD∥BC,点M从A出发,以1cm/s的速度沿射线AD匀速运动,同时点N以相同的速度从C出发沿CB匀速向点B运动,当点N到达B时,点M也停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
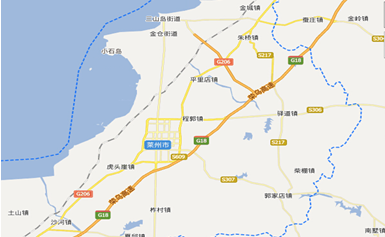
| A. | 金城镇在莱州市中心的北偏东约60°的方向上 | |
| B. | 沙河镇在莱州市中心的南偏西约45°的方向上 | |
| C. | 平里店镇在莱州市中心的南偏西约30°的方向上 | |
| D. | 柞村镇在莱州市中心的南偏东约20°的方向上 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个袋子里有100个同样质地的球,小华摸了8次球,每次都只摸到黑球,这说明袋子里面只有黑球 | |
| B. | 某事件发生的概率为0.5,也就是说,在两次重复的试验中必有一次发生 | |
| C. | 随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率为$\frac{1}{3}$ | |
| D. | 某校九年级有400名学生,一定有2名学生同一天过生日 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com