
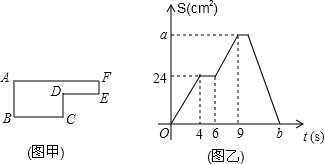
 已知动点P以每秒v厘米的速度沿图甲的边框(边框拐角处都相互垂直)按从B→C→D→E→F→A的路径匀速移动,相应的△PAB的面积S关于时间t的函数图象如图乙.若AB=6cm.根据图象信息回答下列问题:
已知动点P以每秒v厘米的速度沿图甲的边框(边框拐角处都相互垂直)按从B→C→D→E→F→A的路径匀速移动,相应的△PAB的面积S关于时间t的函数图象如图乙.若AB=6cm.根据图象信息回答下列问题: ×6×BC=24,
×6×BC=24, AB•(BC+DE),
AB•(BC+DE), ×6×(8+6)=42(cm2).
×6×(8+6)=42(cm2). AB•(BC+DE),代入数值即可求解;计算BC+CD+DE+EF+FA的长度,又由动点P的速度,计算可得b的值.
AB•(BC+DE),代入数值即可求解;计算BC+CD+DE+EF+FA的长度,又由动点P的速度,计算可得b的值.

科目:初中数学 来源: 题型:
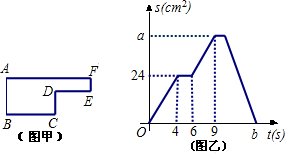 的路径移动,相应的△PAB的面积S关于时间t的函数图象如图乙.若AB=6cm.
的路径移动,相应的△PAB的面积S关于时间t的函数图象如图乙.若AB=6cm.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知动点P以每秒v厘米的速度沿图甲的边框(边框拐角处都相互垂直)按从B→C→D→E→F→A的路径匀速移动,相应的△PAB的面积S关于时间t的函数图象如图乙.若AB=6cm.根据图象信息回答下列问题:
已知动点P以每秒v厘米的速度沿图甲的边框(边框拐角处都相互垂直)按从B→C→D→E→F→A的路径匀速移动,相应的△PAB的面积S关于时间t的函数图象如图乙.若AB=6cm.根据图象信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
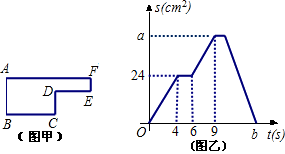 的路径移动,相应的△PAB的面积S关于时间t的函数图象如图乙.若AB=6cm.
的路径移动,相应的△PAB的面积S关于时间t的函数图象如图乙.若AB=6cm.查看答案和解析>>
科目:初中数学 来源:2008年福建省泉州市丰泽区初中学业质量检查数学试卷(解析版) 题型:解答题
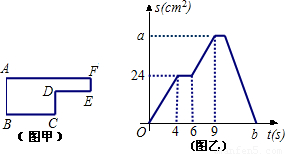
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com