
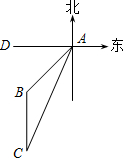
 一条船上午8点在A处望见西南方向有一座灯塔B(如图),此时测得船和灯塔相距36$\sqrt{2}$海里,船以每小时20海里的速度向南偏西24°的方向航行到C处,这时望见灯塔在船的正北方向.(参考数据:sin24°≈0.4,cos24°≈0.9).
一条船上午8点在A处望见西南方向有一座灯塔B(如图),此时测得船和灯塔相距36$\sqrt{2}$海里,船以每小时20海里的速度向南偏西24°的方向航行到C处,这时望见灯塔在船的正北方向.(参考数据:sin24°≈0.4,cos24°≈0.9).分析 (1)要求几点到达C处,需要先求出AC的距离,根据时间=距离除以速度,从而求出解.
(2)船和灯塔的距离就是BC的长,作出CB的延长线交AD于E,根据直角三角形的角,用三角函数可求出CE的长,减去BE就是BC的长.
解答  解:(1)延长CB与AD交于点E,则∠AEB=90°,
解:(1)延长CB与AD交于点E,则∠AEB=90°,
∵∠BAE=45°,AB=36$\sqrt{2}$,
∴BE=AE=36.
根据题意得:∠C=24°,sin24°=$\frac{AE}{AC}$,
∴AC=90.
90÷20=4.5,8+4.5=12.5,
所以12点30分到达C处;
(2)在直角三角形ACE中,cos24°=$\frac{EC}{AC}$,
即cos24°=$\frac{36+BC}{90}$=0.9,
解得BC=45.
所以船到达C处时与灯塔B之间的距离是45海里.
点评 本题考查了解直角三角形的应用-方向角问题,关键理解西南方向,正北方向从而找出角的度数,作出辅助线构成直角三角形从而可求出解.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△AOM中,OA⊥OM,OA=2,以O为圆心,OA为半径作⊙O交AM于N,过点N作⊙O的切线交OM于P,若PM、PN为关于x的一元二次方程x2+(m-2)x+m+1=0的两根,求S△AOM.
如图,△AOM中,OA⊥OM,OA=2,以O为圆心,OA为半径作⊙O交AM于N,过点N作⊙O的切线交OM于P,若PM、PN为关于x的一元二次方程x2+(m-2)x+m+1=0的两根,求S△AOM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com