
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
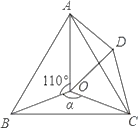
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
【答案】(1)详见解析;(2)△AOD是直角三角形,理由详见解析;(3)当α=110°或125°或140°时,△AOD是等腰三角形.
【解析】
(1)根据全等三角形的性质得到OC=DC,根据等边三角形的判定定理证明即可;
(2)根据全等三角形的性质得到∠ADC=∠BOC=∠α=150°,结合图形计算即可;
(3)分∠AOD=∠ADO、∠AOD=∠OAD、∠ADO=∠OAD三种情况,根据等腰三角形的判定定理计算即可.
解:(1)∵△BOC≌△ADC,
∴OC=DC.
∵∠OCD=60°,
∴△OCD是等边三角形.
(2)△AOD是直角三角形.
理由如下:
∵△OCD是等边三角形,
∴∠ODC=60°,
∵△BOC≌△ADC,∠α=150°,
∴∠ADC=∠BOC=∠α=150°,
∴∠ADO=∠ADC﹣∠ODC=150°﹣60°=90°,
∴△AOD是直角三角形.
(3)∵△OCD是等边三角形,
∴∠COD=∠ODC=60°.
∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360°﹣∠AOB﹣∠BOC﹣∠COD=360°﹣110°﹣α﹣60°=190°﹣α,
∠ADO=∠ADC﹣∠ODC=α﹣60°,
∴∠OAD=180°﹣∠AOD﹣∠ADO=180°﹣(190°﹣α)﹣(α﹣60°)=50°.
①当∠AOD=∠ADO时,190°﹣α=α﹣60°,
∴α=125°.
②当∠AOD=∠OAD时,190°﹣α=50°,
∴α=140°.
③当∠ADO=∠OAD时,
α﹣60°=50°,
∴α=110°.
综上所述:当α=110°或125°或140°时,△AOD是等腰三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
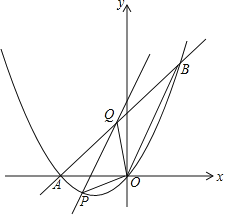
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于原点及点A,且经过点B(4,8),对称轴为直线x=﹣2.
(1)求抛物线的解析式;
(2)设直线y=kx+4与抛物线两交点的横坐标分别为x1,x2(x1<x2),当![]() 时,求k的值;
时,求k的值;
(3)连接OB,点P为x轴下方抛物线上一动点,过点P作OB的平行线交直线AB于点Q,当S△POQ:S△BOQ=1:2时,求出点P的坐标.
(坐标平面内两点M(x1,y1),N(x2,y2)之间的距离MN=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瑞士的一位中学教师巴尔末从光谱数据![]() ,
,![]() ,
,![]() ,
,![]() …中,成功地发现了其规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据这个规律写出第6个数为____.
…中,成功地发现了其规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据这个规律写出第6个数为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 .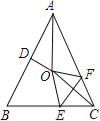
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现思考:已知等腰三角形ABC的两边分别是方程x2﹣7x+10=0的两个根,求等腰三角形ABC三条边的长各是多少?下边是涵涵同学的作业,老师说他的做法有错误,请你找出错误之处并说明错误原因.
涵涵的作业
解:x2﹣7x+10=0
a=1 b=﹣7 c=10
∵b2﹣4ac=9>0
∴x=![]() =
=![]()
∴x1=5,x2=2
所以,当腰为5,底为2时,等腰三角形的三条边为5,5,2.
当腰为2,底为5时,等腰三角形的三条边为2,2,5.
探究应用:请解答以下问题:
已知等腰三角形ABC的两边是关于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的两个实数根.
=0的两个实数根.
(1)当m=2时,求△ABC的周长;
(2)当△ABC为等边三角形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF; ②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F; ④AB=DE,AC=DF,∠B=∠E.能使△ABC≌△DEF有_____组.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示的是用火柴棒搭成的一个个图形,第一个图形用了5根火柴,第二个图形用了8根火柴,…,用281根火柴棒搭成了第( )个图形.
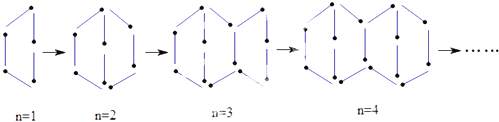
A. 93 B. 94 C. 80 D. 81
查看答案和解析>>
科目:初中数学 来源: 题型:
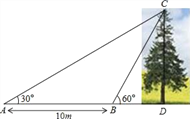
【题目】如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
【答案】8.7米
【解析】试题分析:首先利用三角形的外角的性质求得∠ACB的度数,得到BC的长度,然后在直角△BDC中,利用三角函数即可求解.
试题解析:∵∠CBD=∠A+∠ACB,
∴∠ACB=∠CBD﹣∠A=60°﹣30°=30°,
∴∠A=∠ACB,
∴BC=AB=10(米).
在直角△BCD中,CD=BCsin∠CBD=10×![]() =5
=5![]() ≈5×1.732=8.7(米).
≈5×1.732=8.7(米).
答:这棵树CD的高度为8.7米.
考点:解直角三角形的应用
【题型】解答题
【结束】
23
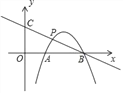
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+ax+b交x轴于A(1,0),B(3,0)两点,点P是抛物线上在第一象限内的一点,直线BP与y轴相交于点C.
(1)求抛物线y=﹣x2+ax+b的解析式;
(2)当点P是线段BC的中点时,求点P的坐标;
(3)在(2)的条件下,求sin∠OCB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】|a|+|b|=|a+b|,则a,b关系是( )
A. a,b的绝对值相等
B. a,b异号
C. a+b的和是非负数
D. a、b同号或a、b其中一个为0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com