
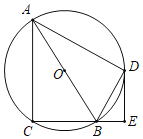
【题目】小明在学习“圆的对称性”时知道结论:垂直于弦的直径一定平分这条弦,请尝试解决问题:如图,在Rt△ACB中,∠ACB=90°,圆O是△ACB的外接圆.点D是圆O上一点,过点D作DE⊥BC,垂足为E,且BD平分∠ABE,
(1)判断直线ED与圆O的位置关系,并说明理由.
(2)若AC=12,BC=5,求线段BE的长.
【答案】(1)直线ED与⊙O相切,见解析;(2)4
【解析】
(1)直线ED与⊙O相切.连接OD.根据圆的性质和等边对等角可得∠ODB=∠OBD,等量代换得到∠ODB=∠DBE,根据平行线的判定和性质得到∠DEC=∠ODE=90°,再根据垂直的定义和性质可得OD⊥DE,根据切线的判定即可求解;
(2)如图,延长DO交AC于点H,连结CO,构建直角△ABC的中位线OH,运用三角形中位线定理和勾股定理分别求得OH=HO=![]() BC=
BC=![]() 、AB=13,结合图形找到相关线段间的和差关系求得线段BE的长度即可.
、AB=13,结合图形找到相关线段间的和差关系求得线段BE的长度即可.
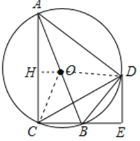
(1)如图,连接OD.
∵OB=OD,
∴∠ODB=∠OBD,
又∵∠OBD=∠DBE,
∴∠ODB=∠DBE,
∴OD∥BE,
又∵DE⊥BC,
∴∠DEC=90°,
∴∠ODE=90°,
∴OD⊥DE,
又∵OD为半径,
∴直线ED与⊙O相切;
(2)如图,延长DO交AC于点H,连结CO,
∵OD∥BE,∠ODE=90°,
∴∠OHC=90°,即OH⊥AC,
又∵OA=OC,
∴AH=CH,又由O是AB的中点,
∴HO是△ABC的中位线,
∴HO=![]() BC=
BC=![]() .
.
∵AC为直径,
∴∠ACB=90°,
∴AC=12,BC=5,
∴AB=![]() =
=![]() =13,
=13,
∴OA=OD=![]() AB=
AB=![]() .
.
∴HD=HO+OD=9
由四边形CEDH是矩形,
∴CE=HD=9,
∴CE=9,
∴BE=CE﹣BC=4.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 、
、![]() .
.
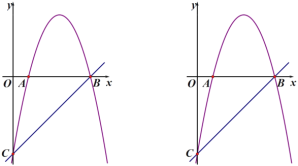
(1)求抛物线的函数表达式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的一动点,求
上方抛物线上的一动点,求![]() 面积
面积![]() 的最大值并求出此时点
的最大值并求出此时点![]() 的坐标;
的坐标;
(3)过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() ,连接
,连接![]() ,当直线
,当直线![]() 与直线
与直线![]() 的一个夹角等于
的一个夹角等于![]() 的3倍时,请直接写出点
的3倍时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为2,弦AB的长为2![]() ,点C是优弧AB上的一动点,BD⊥BC交直线AC于点D,当点C从△ABC面积最大时运动到BC最长时,点D所经过的路径长为_____.
,点C是优弧AB上的一动点,BD⊥BC交直线AC于点D,当点C从△ABC面积最大时运动到BC最长时,点D所经过的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
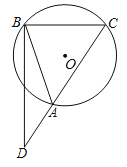
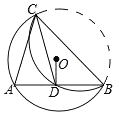
【题目】如图,在⊙O中,点C在优弧![]() 上,将
上,将![]() 沿BC折叠后刚好经过AB的中点D,连接AC,CD.则下列结论中错误的是( )
沿BC折叠后刚好经过AB的中点D,连接AC,CD.则下列结论中错误的是( )
①AC=CD;②AD=BD;③![]() +
+![]() =
=![]() ;④CD平分∠ACB
;④CD平分∠ACB
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读,我们可以用换元法解简单的高次方程,解方程x4﹣3x2+2=0时,可设y=x2,则原方程可比为y2+3y+2=0,解之得y1=2,y2=1,当y1=2时,则x2=2,即x1=![]() ,x2=﹣
,x2=﹣![]() ;当y2=1时,即x2=1,则x1=1,x2=﹣1,故原方程的解为x1=
;当y2=1时,即x2=1,则x1=1,x2=﹣1,故原方程的解为x1=![]() ,x2=﹣
,x2=﹣![]() ,x3=1,x4=﹣1,仿照上面完成下面解答:
,x3=1,x4=﹣1,仿照上面完成下面解答:
(1)已知方程(2x2+1)2+2x2﹣3=0,设y=2x2+1,则原方程可化为_______.
(2)仿照上述解法解方程:(x2﹣2x)2﹣3x2+6x=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为1,弦AB=![]() ,BC=
,BC=![]() ,AB,BC在圆心O的两侧,弧AC上有一动点D,AE⊥BD于点E,当点D从点C运动到点A时,则点E所经过的路径长为__________.
,AB,BC在圆心O的两侧,弧AC上有一动点D,AE⊥BD于点E,当点D从点C运动到点A时,则点E所经过的路径长为__________.
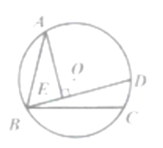
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形MNPQ中,动点R从点N出发,沿着N-P-Q-M方向移动至M停止,设R移动路程为x,MNR面积为y,那么y与x的关系如图②,下列说法不正确的是( )

A.当x=2时,y=5B.矩形MNPQ周长是18
C.当x=6时,y=10D.当y=8时,x=10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次数学竞赛共有3道判断题,认为正确的写“![]() ”,错误的写“
”,错误的写“![]() ”,小明在做判断题时,每道题都在“
”,小明在做判断题时,每道题都在“![]() ”或“
”或“![]() ”中随机写了一个.
”中随机写了一个.
(1)小明做对第1题的概率是 ;
(2)求小明这3道题全做对的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com