
 小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B、C、D三点在同一直线上.
小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B、C、D三点在同一直线上.分析 (1)设DE=x,可得EF=DE-DF=x-2,从而得AF=$\frac{EF}{tan∠EAF}$=$\sqrt{3}$(x-2),再求出CD=$\frac{DE}{tan∠DCE}$=$\frac{\sqrt{3}}{3}$x、BC=$\frac{AB}{tan∠ACB}$=2$\sqrt{3}$,根据AF=BD可得关于x的方程,解之可得;
(2)延长NM交DB延长线于点P,知AM=BP=3,由(1)得CD=$\frac{\sqrt{3}}{3}$x=2$\sqrt{3}$、BC=2$\sqrt{3}$,根据NP=PD且AB=MP可得答案.
解答 解:(1)如图,设DE=x,
∵AB=DF=2,
∴EF=DE-DF=x-2,
∵∠EAF=30°,
∴AF=$\frac{EF}{tan∠EAF}$=$\frac{x-2}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$(x-2),
又∵CD=$\frac{DE}{tan∠DCE}$=$\frac{x}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$x,BC=$\frac{AB}{tan∠ACB}$=$\frac{2}{\frac{\sqrt{3}}{3}}$=2$\sqrt{3}$,
∴BD=BC+CD=2$\sqrt{3}$+$\frac{\sqrt{3}}{3}$x
由AF=BD可得$\sqrt{3}$(x-2)=2$\sqrt{3}$+$\frac{\sqrt{3}}{3}$x,
解得:x=6,
∴树DE的高度为6米;
(2)延长NM交DB延长线于点P,则AM=BP=3,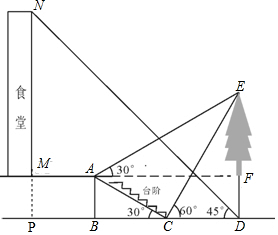
由(1)知CD=$\frac{\sqrt{3}}{3}$x=$\frac{\sqrt{3}}{3}$×6=2$\sqrt{3}$,BC=2$\sqrt{3}$,
∴PD=BP+BC+CD=3+2$\sqrt{3}$+2$\sqrt{3}$=3+4$\sqrt{3}$,
∵∠NDP=45°,且MP=AB=2,
∴NP=PD=3+4$\sqrt{3}$,
∴NM=NP-MP=3+4$\sqrt{3}$-2=1+4$\sqrt{3}$,
∴食堂MN的高度为1+4$\sqrt{3}$米.
点评 本题考查了解直角三角形的应用,解题的关键是正确的构造直角三角形并选择正确的边角关系解直角三角形.


科目:初中数学 来源: 题型:解答题
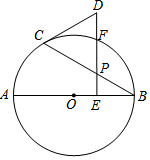 如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.
如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
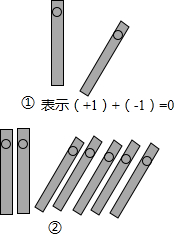 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为-3.
中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
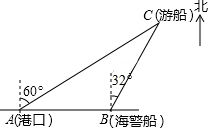 (7分)一艘游船从港口A处以北偏东60°的方向出港观光.航行170海里至C处时发生了事故.船长立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东32°方向.若海警船以60海里/时的速度前往救援,求海警船到达事故船C处大约所需的时间.(精确到0.1小时)【参考数据:sin32°=0.53,cos32°=0.85.tan32°=0.62】
(7分)一艘游船从港口A处以北偏东60°的方向出港观光.航行170海里至C处时发生了事故.船长立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东32°方向.若海警船以60海里/时的速度前往救援,求海警船到达事故船C处大约所需的时间.(精确到0.1小时)【参考数据:sin32°=0.53,cos32°=0.85.tan32°=0.62】查看答案和解析>>
科目:初中数学 来源: 题型:选择题
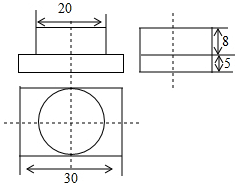 如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )
如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )| A. | 800π+1200 | B. | 160π+1700 | C. | 3200π+1200 | D. | 800π+3000 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com