
����Ŀ����ͼ1��E�ǵȱ�������ABC�ı�AB����ֱ����һ�㣬D�DZ�BC����ֱ����һ�㣬��D��C���غϣ���EC��ED�����DΪ��C���ڵȱ�������ABC�ķ��Ƶ㣬��E��Ϊ�������ģ�
��ƽ��ֱ������ϵxOy�У�
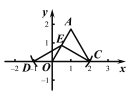
��1����֪�ȱ�������AOC�Ķ���C������Ϊ��2��0������A�ڵ�һ�����ڣ���������E��ֱ��AO�ϣ����Ƶ�D��ֱ��OC�ϣ�
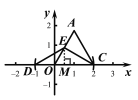
����ͼ2����EΪ��AO���е㣬��ͼ��������C���ڵȱ�������AOC�ķ��Ƶ�D����ֱ��д����D�����꣺�� ����
����AE��2�����C���ڵȱ�������AOC�ķ��Ƶ�D�����ꣻ
��2�����ȱ�������ABC�Ķ���ΪB��n��0����C��n+1��0������������E��ֱ��AB�ϣ����Ƶ�D��ֱ��BC�ϣ���2��AE��3����ֱ��д����C���ڵȱ�������ABC�ķ��Ƶ�D�ĺ�����t��ȡֵ��Χ���� �����ú�n�Ĵ���ʽ��ʾ����

���𰸡�(1)��D��-1,0��; ��D(![]() 2,0);(2)
2,0);(2) ![]() ��
��![]()
��������
��1���ٸ������з��Ƶ��뷴�����ĵĶ���������D���ɵ����ꣻ
����AO=OC=2����AE=2,��E����������ܵ�λ�ã���ͼ3��ͼ4�����ۣ��ɵ�D���ֵ��
(2)�ɣ�1���ɵ÷��Ƶ��뷴�����ĵĹ��ɣ���B(n,0)��C(n+1,0)��2��AE<3�ɵ�![]() ��
��![]() .
.
��1���� ��ͼ��
 ��
�� 
D(-1,0)
�� �ߵȱ�������AOC����������ΪO(0,0)��C(2,0),
��OC=2.
��AO=OC=2.
��AE=2��֪����E���������ܵ�λ�ã���ͼ3��ͼ4��.
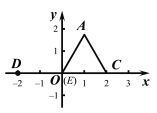

ͼ3 ͼ4
(��) ��ͼ3����E������ԭ��O�غ�.
��EC=ED��EC=2,
��ED=2.
��D�DZ�OC����ֱ����һ�㣬��D��C���غ�,
��D������Ϊ(![]() 2,0) .
2,0) .
(��) ��ͼ4����E�ڱ�OA���ӳ����ϣ���AE=2.
��AC=AE=2,
���E=��ACE.
�ߡ�AOCΪ�ȱ�������,
���OAC =��ACO=60��.
���E=��ACE=30��.
���OCE=90��.
��EC=ED,
���D���C�غ�.
������Ŀ�����е�D��C���غ�ì�ܣ�����ͼ4�е����������Ҫ����ȥ.
����������D(![]() 2,0). ��
2,0). ��
��2��![]() ��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����Сǿ���а������ܣ�С����Сǿ�ܵÿ죬�������ͬʱ���ܣ�С���϶�Ӯ����ͼ��ʾ������С����Сǿ����_______�ף�ֱ��__________��ʾС����·����ʱ��Ĺ�ϵ����Լ_______��ʱ��С������Сǿ��Сǿ����������е��ٶ���________ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ľߵ���1050Ԫ������һ��ij�ֱָ�,�ܿ�����,����1440Ԫ�����ڶ������ֱָ�,���ڶ���ÿ֧�ֱʵĽ����ǵ�һ�����۵�1.2��,�����ȵ�һ������10֧��
(1)���һ��ÿ֧�ֱʵĽ����Ƕ���Ԫ?
(2)�ڶ����ֱʰ�24Ԫ/֧�ļ۸�����,����һ��������,�����г����,�̵������ʣ��ĸֱ�ȫ��8��һ���Դ�������,��Ҫ��ڶ����ֱʵ������ʲ�����20%,���������۶���֧��ʼ����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+bx+c����B��3��0����C��0��3����DΪ�����ߵĶ��㣮
��1���������ߵĽ���ʽ�Լ��������ꣻ
��2�������C����������y=��x2+bx+c�Գ���ĶԳƵ�ΪE�㣬����BC��BE����tan��CBE��ֵ��
��3����M�������߶Գ�����һ�㣬�ҡ�DAM�͡�BCE���ƣ����M���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�������������ͼ������ͼ���ǵױ߳�Ϊ6����Ϊ4�ĵ��������Σ�����ͼ��һ��Բ����ô���������IJ�����ǣ� �� 
A.12��
B.24��
C.![]() ��
��
D.15��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���![]() ��
��![]() ����
����![]() �ڵ������ޣ���֪
�ڵ������ޣ���֪![]() ����
����![]() ��
��
��1�����![]() �����ꣻ
�����ꣻ
ͼ1
��2����ͼ2��![]() Ϊ�߶�
Ϊ�߶�![]() ��һ���㣨�˵���⣩��
��һ���㣨�˵���⣩��![]() ��
��![]() �Ḻ�����һ�㣬����
�Ḻ�����һ�㣬����![]() ��
��![]() ������
������![]() ��
��![]() �Ľ�ƽ���߽���
�Ľ�ƽ���߽���![]() ����
����![]() �����
�����![]() �����ꣻ
�����ꣻ
ͼ2
��3���ڵڣ�2���ʵĻ����ϣ���ͼ3����![]() ���
���![]() ����
����![]() ��Գƣ�
��Գƣ�![]() ������
������![]() ��һ�����㣬����
��һ�����㣬����![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ������
������![]() ������
������![]() �Ķ����Ƿ����ı䣿�����䣬��������������ı䣬��ָ����仯��Χ��
�Ķ����Ƿ����ı䣿�����䣬��������������ı䣬��ָ����仯��Χ��
ͼ3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC��BC���ϵ�����ADƽ�Ƶ���A'B'C'��λ�ã���֪��ABC�����Ϊ9����Ӱ���������ε����Ϊ4����AA'=1����A'D���ڣ�������

A. 2 B. 3 C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABCD��AD����ƽ�Ƶ�����EFGH��HG=24cm��WG=8cm��CW=6cm������Ӱ���������
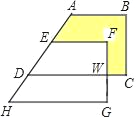
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com