
 直线y=x+4分别与x轴、y轴交于点M、N,边长为2的正方形OABC一个顶点O在坐标原点,直线AN与MC相交于点P,若正方形OABC绕着点O旋转一周,点P的位置也发生变化,则点P到点(0,2)距离的最小值为2$\sqrt{2}$-2.
直线y=x+4分别与x轴、y轴交于点M、N,边长为2的正方形OABC一个顶点O在坐标原点,直线AN与MC相交于点P,若正方形OABC绕着点O旋转一周,点P的位置也发生变化,则点P到点(0,2)距离的最小值为2$\sqrt{2}$-2. 分析 首先证明△MOC≌△NOA,推出∠MPN=90°,推出P在以MN为直径的圆上,所以当圆心G,点P,C(0,2)三点共线时,P到C(0,2)的最小值.求出此时的PC即可.
解答 解:在△MOC和△NOA中, $\left\{\begin{array}{l}{OA=OC}\\{∠MOC=∠AON}\\{OM=ON}\end{array}\right.$,
$\left\{\begin{array}{l}{OA=OC}\\{∠MOC=∠AON}\\{OM=ON}\end{array}\right.$,
∴△MOC≌△NOA,
∴∠CMO=∠ANO,
∵∠CMO+∠MCO=90°,∠MCO=∠NCP,
∴∠NCP+∠CNP=90°,
∴∠MPN=90°
∴MP⊥NP,
在正方形旋转的过程中,同理可证,∴∠CMO=∠ANO,可得∠MPN=90°,MP⊥NP,
∴P在以MN为直径的圆上,
∵M(-4,0),N(0,4),
∴圆心G为(-2,2),半径为2$\sqrt{2}$,
∵PG-GC≤PC,
∴当圆心G,点P,C(0,2)三点共线时,PC最小,
∵GN=GM,CN=CO=2,
∴GC=$\frac{1}{2}$OM=2,
这个最小值为GP-GC=2$\sqrt{2}$-2.
故答案为:2$\sqrt{2}$-2.
点评 本题考查一次函数与几何变换、正方形的性质、圆的有关知识,解题的关键是发现点P在以MN为直径的圆上,确定点P的位置是解题的关键,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知A、B两点的坐标分别为(2$\sqrt{3}$,0)(0,2),P是△AOB外接圆上的一点,且∠AOP=30°,则点P的坐标为(1,$\sqrt{3}$)或(2,2$\sqrt{3}$).
如图,已知A、B两点的坐标分别为(2$\sqrt{3}$,0)(0,2),P是△AOB外接圆上的一点,且∠AOP=30°,则点P的坐标为(1,$\sqrt{3}$)或(2,2$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
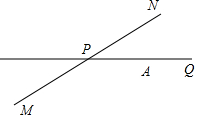 如图所示,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所学校,AP=160m,假设一拖拉机在公路MN上沿PN方向行驶,周围100m内会受到杂音的影响,如果拖拉机的速度为18km/h,则学校受到影响的时间有多长?
如图所示,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所学校,AP=160m,假设一拖拉机在公路MN上沿PN方向行驶,周围100m内会受到杂音的影响,如果拖拉机的速度为18km/h,则学校受到影响的时间有多长?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com