
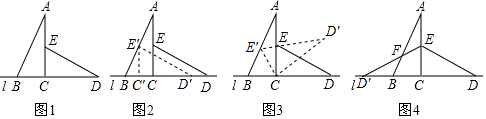
·ÖĪö £Ø1£©ĻČÅŠ¶Ļ³öC'E'=3£¬ŌŁĄūÓĆŗ¬30¶Č½ĒµÄÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆ³öBE'=2BC£¬×īŗóÓĆ¹“¹É¶ØĄķĒó³öBC'¼“æÉµĆ³ö½įĀŪ£®
£Ø2£©”÷ECDČʵćCŠż×ŖµÄ¶ČŹż¼“”ĻECE'µÄ¶ČŹż£»Ņ×µĆ£ŗ”ĻECE”ä=”ĻBAC=30”ć£»
£Ø3£©øł¾ŻĢõ¼ž£¬Ö¤Ć÷”÷AEF”Õ”÷D”äBF½ų¶ųµĆ³öAF=FD”ä
½ā“š £Ø1£©½ā£ŗCC”ä=3-$\sqrt{3}$£®
ĄķÓÉČēĻĀ£ŗÓÉĘ½ŅĘÖŖ£¬C'E'”ĪAC£¬C'E'=CE=3£¬
”ą”ĻBE'C'=”ĻA=30”ć£¬
”ßBC=EC=3£¬
ŌŚRt”÷BC'E'ÖŠ£¬”ĻBE'C'=30”ć£¬
øł¾ŻŌŚÖ±½ĒČż½ĒŠĪÖŠ£¬30”ć½ĒĖł¶ŌµÄÖ±½Ē±ßŹĒŠ±±ßµÄŅ»°ė£¬µĆBE'=2BC'
”ąBE'2-BC'2=C'E'2£¬
¼“£ŗ4BC'2-BC'2=9£¬
”ąBC'=$\sqrt{3}$£¬
”ąCC”ä=BC-BC'=3-$\sqrt{3}$£»
¹Ź“š°øĪŖ£ŗ3-$\sqrt{3}$£»
£Ø2£©½ā£ŗ”÷ECDČʵćCŠż×ŖµÄ¶ČŹż¼“”ĻECE”äµÄ¶ČŹż£»
”ß”ĻABC=60”ć£¬BC=CE”ä=3£¬AB=6£¬
”ą”÷E”äBCŹĒµČ±ßČż½ĒŠĪ£¬
”ąBC=E”äC=E”äB=3£¬
”ąAE”ä=E”äC=3£¬
”ą”ĻE”äAC=”ĻE”äCA£¬
”ą”ĻECE”ä=”ĻBAC=30”ć£»
¹Ź“š°øĪŖ£ŗ30”ć£»
£Ø3£©Ö¤Ć÷£ŗŌŚ”÷AEFŗĶ”÷D”äBFÖŠ£¬
”ßAE=AC-EC£¬D”äB=D”äC-BC£¬
ÓÖ”ßAC=D”äC£¬EC=BC£¬
”ąAE=D”äB£¬
Ó֔ߔĻAEF=”ĻD”äBF=180”ć-60”ć=120”ć£¬”ĻA=”ĻCD”äE=30”ć£¬
”ą”÷AEF”Õ”÷D”äBF£¬
”ąAF=FD'
µćĘĄ ±¾Ģāæ¼²éĘ½ŅĘ”¢Šż×ŖµÄŠŌÖŹ£»Ę½ŅʵĻł±¾ŠŌÖŹŹĒ£ŗ¢ŁĘ½ŅĘ²»øıäĶ¼ŠĪµÄŠĪדŗĶ“󊔣»¢Ś¾¹żĘ½ŅĘ£¬¶ŌÓ¦µćĖłĮ¬µÄĻ߶ĪĘ½ŠŠĒŅĻąµČ£¬¶ŌÓ¦Ļ߶ĪĘ½ŠŠĒŅĻąµČ£¬¶ŌÓ¦½ĒĻąµČ£®Šż×Ŗ±ä»ÆĒ°ŗ󣬶ŌÓ¦Ļ߶Ī”¢¶ŌÓ¦½Ē·Ö±šĻąµČ£¬Ķ¼ŠĪµÄ“óŠ””¢ŠĪד¶¼²»øı䣬Į½×é¶ŌÓ¦µćĮ¬ĻߵĽ»µćŹĒŠż×ŖÖŠŠÄ£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | $\sqrt{3}$ŹĒ3µÄĘ½·½øł | B£® | |$\sqrt{2}$-1|=$\sqrt{2}$-1 | ||
| C£® | -$\sqrt{5}$µÄĻą·“ŹżŹĒ$\sqrt{5}$ | D£® | “ųøłŗÅµÄŹż¶¼ŹĒĪŽĄķŹż |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com