
【题目】小李去买套装![]() 色水笔和笔记本,若购买
色水笔和笔记本,若购买![]() 袋笔和
袋笔和![]() 本笔记本,他身上的钱还差
本笔记本,他身上的钱还差![]() 元,若改 成购买
元,若改 成购买![]() 袋笔和
袋笔和![]() 本笔记本,他身上的钱会剩下
本笔记本,他身上的钱会剩下![]() 元.若他把身上的钱都花掉,购买这两种 物品(两种都买)的方案有( )
元.若他把身上的钱都花掉,购买这两种 物品(两种都买)的方案有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
【答案】C
【解析】
设1袋笔的价格为x元,1本笔记本的价格为y元,根据“若购买4袋笔和6本笔记本,他身上的钱还差22元,若改成购买1袋笔和2本笔记本,他身上的钱会剩下34元”,即可得出关于x,y的二元一次方程,结合x,y均为正整数即可得出结论,再设可购买a袋笔和b本笔记本,根据总价=单价×数量可得出关于a,b的二元一次方程,结合a,b均为正整数即可得出结论.
设1袋笔的价格为x元,1本笔记本的价格为y元,
依题意,得:4x+6y-22=x+2y+34,
∴3x+4y=56,即y=14-![]() x.
x.
∵x,y均为正整数,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
设可购买a袋笔和b本笔记本.
①当x=4,y=11时,4x+6y-22=60,
∴4a+11b=60,即a=15-![]() b,
b,
∵a,b均为正整数,
∴![]() ;
;
②当x=8,y=8时,4x+6y-22=58,
∴8a+8b=58,即a+b=![]() ,
,
∵a,b均为正整数,
∴方程无解;
③当x=12,y=5时,4x+6y-22=56,
∴12a+5b=56,即b=![]() ,
,
∵a,b均为正整数,
∴![]() ;
;
④当x=16,y=2时,4x+6y-22=54,
∴16a+2b=54,即b=27-8a,
∵a,b均为正整数,
∴![]() ,
,![]() ,
,![]() .
.
综上所述,共有5种购进方案.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,∠B=90°,
中,∠B=90°,![]() ,点D,E分别是边BC,AC的中点,连接
,点D,E分别是边BC,AC的中点,连接![]() 将
将![]() 绕点C按顺时针方向旋转,记旋转角为
绕点C按顺时针方向旋转,记旋转角为![]() .
.
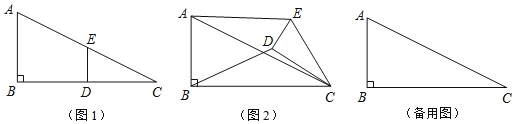
![]() 问题发现:
问题发现:
![]() 当
当![]() 时,
时,![]() _____;
_____;![]() 当
当![]() 时,
时,![]() _____.
_____.
![]() 拓展探究:
拓展探究:
试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
![]() 问题解决:
问题解决:
当![]() 旋转至A、D、E三点共线时,直接写出线段BD的长.
旋转至A、D、E三点共线时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
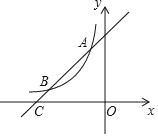
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求a,k的值及点B的坐标;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,直接写出点P的坐标.
S△BOC,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
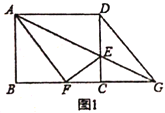
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠,顶点
折叠,顶点![]() 恰好落在
恰好落在![]() 边上点
边上点![]() 处,延长
处,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)求![]() 的值;
的值;
(2)求证:四边形![]() 是菱形;
是菱形;
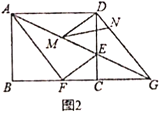
(3)如图2,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上的动点(与端点不重合),且
上的动点(与端点不重合),且![]() ,设
,设![]() ,
,![]() ,请解决以下相关问题:
,请解决以下相关问题:
①写出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
②是否存在这样的点![]() ,使
,使![]() 是等腰三角形?若存在,请求出
是等腰三角形?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学课外实践小组一次活动中,测量一座楼房的高度.如图,在山坡坡脚A处测得这座楼房的楼顶B点的仰角为60°,沿山坡往上走到C处再测得B点的仰角为45°,已知山坡的坡比i=1:![]() ,OA=200m,且O、A、D在同一条直线上.
,OA=200m,且O、A、D在同一条直线上.
(1)求楼房OB的高度;
(2)求山坡上AC的距离(结果保留根号)
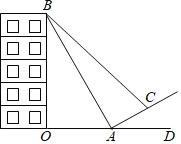
查看答案和解析>>
科目:初中数学 来源: 题型:
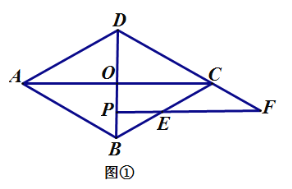
【题目】已知菱形![]() 的对角线交于点
的对角线交于点![]() 是直线
是直线![]() 上任意一点(异于点
上任意一点(异于点![]() ),过点
),过点![]() 作平行于
作平行于![]() 的直线交直线
的直线交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)当点![]() 在线段
在线段![]() 上时,如图 ①,易证:
上时,如图 ①,易证:![]() (不用证明);
(不用证明);
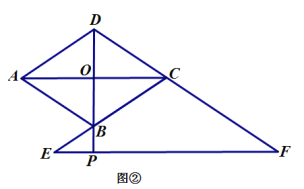
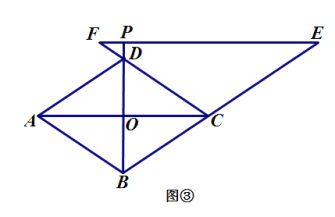
(2)当点![]() 在线段
在线段![]() 的延长线上时,如图 ②;当点
的延长线上时,如图 ②;当点![]() 在线段
在线段![]() 的延长线上时,如图 ③,线段
的延长线上时,如图 ③,线段![]() 之间又有怎样的数量关系? 请写出你的猜想,并选择其中一种情况加以证明.
之间又有怎样的数量关系? 请写出你的猜想,并选择其中一种情况加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更新果树品种,某果园计划新购进![]() 、
、![]() 两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中
两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中![]() 种苗的单价为
种苗的单价为![]() 元/棵,购买
元/棵,购买![]() 种苗所需费用
种苗所需费用![]() (元)与购买数量
(元)与购买数量![]() (棵)之间存在如图所示的函数关系.
(棵)之间存在如图所示的函数关系.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若在购买计划中,![]() 种苗的数量不超过35棵,但不少于
种苗的数量不超过35棵,但不少于![]() 种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列动车从甲地开往乙地, 一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为![]() (小时),两车之间的距离为
(小时),两车之间的距离为![]() (千米),如图中的折线表示
(千米),如图中的折线表示![]() 与
与![]() 之间的函数关系,下列说法:①动车的速度是
之间的函数关系,下列说法:①动车的速度是![]() 千米/小时;②点B的实际意义是两车出发后
千米/小时;②点B的实际意义是两车出发后![]() 小时相遇;③甲、乙两地相距
小时相遇;③甲、乙两地相距![]() 千米;④普通列车从乙地到达甲地时间是
千米;④普通列车从乙地到达甲地时间是![]() 小时,其中不正确的有( )
小时,其中不正确的有( )
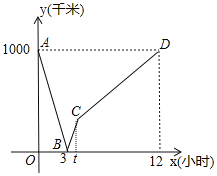
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上一个动点,设点
是抛物线上一个动点,设点![]() 的横坐标为
的横坐标为![]() .连接
.连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
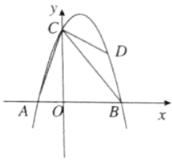
(1)求抛物线的函数表达式;
(2)![]() 的面积何时最大?求出此时
的面积何时最大?求出此时![]() 点的坐标和最大面积;
点的坐标和最大面积;
(3)在(2)的条件下,若点![]() 是
是![]() 轴上一动点,点
轴上一动点,点![]() 是抛物线上一动点,试判断是否存在这样的点
是抛物线上一动点,试判断是否存在这样的点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com