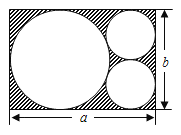
【题目】如图，在一张长为a、宽为b的长方形纸片上，剪掉一个大圆和两个半径相等的小圆．
（1）列出剩余纸片（图中阴影部分）面积的代数式；（结果要求化简）
（2）当a＝6cm，b＝4cm时，求阴影部分的面积，（π取3.14）
【答案】（1）ab﹣0.375πb2；（2）5.16（cm2）
【解析】
（1）根据图示，大圆、小圆的直径分别是b、0.5b，用长方形纸片的面积减去一个大圆和两个半径相等的小圆的面积，列出剩余纸片（图中阴影部分）面积的代数式即可；（2）把a＝6cm，b＝4cm代入（1）求出的代数式，求出阴影部分的面积是多少即可．
解：（1）大圆、小圆的直径分别是b、0.5b，
ab﹣π×（0.5b）2﹣2π×（0.25b）2
＝ab﹣0.25πb2﹣0.125πb2
＝ab﹣0.375πb2
（2）当a＝6cm，b＝4cm时，
阴影部分的面积是：
ab﹣0.375πb2
＝6×4﹣0.375×3.14×42
＝24﹣18.84
＝5.16（cm2）
海淀黄冈名师导航系列答案科目：初中数学 来源： 题型：
【题目】正方形ABCD中，△ADF绕着点A顺时针旋转90°后得到△ABM，点M、B、C在一条直线上，且△AEM与△AEF恰好关于AE所在直线成轴对称。已知EF=7，正方形边长为8。
（1）写出图中形状、大小都相等的三角形
（2）求△EFC的面积。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的方程
＝x+
与
＝6x﹣2的解互为倒数，
（1）求m的值．
（2）若当y＝m时，代数式ay3+by+1的值为5，求当y＝﹣m时，代数式ay3+by+1的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：
（1）23﹣17﹣（﹣7）+（﹣16）
（2）
（3）﹣22÷（﹣4）3+|0.8﹣1|×（2
）2
（4）4xy+（3y2﹣2x2）﹣（5xy﹣2x2）﹣4y2
（5）先化简，再求值：x﹣2（x﹣y2）+（﹣
x+
y2），其中x＝﹣
，y＝3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，对角线AC与BD相交于点O，不能判断四边形ABCD是平行四边形的是（ ）
A. AB∥DC，AD=BC B. AB∥DC，AD∥BC C. AB=DC，AD=BC D. OA=OC，OB=OD
查看答案和解析>>
科目：初中数学 来源： 题型：
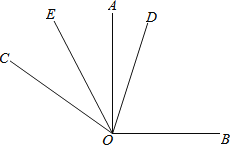
【题目】如图，已知同一平面内∠AOB＝90°，∠AOC＝60°．
（1）问题发现：∠BOD的余角是 ，∠BOC的度数是 ；
（2）拓展探究：若OD平分∠BOC，OE平分∠AOC，则∠DOE的度数是 ；
（3）类比延伸：在（2）条件下，如果将题目中的∠AOB＝90°改为∠AOB＝2∠β；∠AOC＝60°改为∠AOC＝2α（α＜45°），其他条件不变，你能求出∠DOE吗？若能，请你写出求解过程：若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在数轴上点A表示数a，点C表示数c，且
.我们把数轴上两点之间的距离用表示两点的大写字母一起标记.
比如，点A与点B之间的距离记作AB.
(1)求AC的值；
(2)若数轴上有一动点D满足CD＋AD=36，直接写出D点表示的数；
(3)动点B从数1对应的点开始向右运动，速度为每秒1个单位长度，同时点A，C在数轴上运动，点A、C的速度分别为每秒 3个单位长度，每秒4个单位长度，运动时间为t秒.
①若点A向右运动，点C向左运动，AB=BC，求t的值.
②若点A向左运动，点C向右运动，2AB－m×BC的值不随时间t的变化而改变，请求出m的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，图象中所反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后，又 去早餐店吃早餐，然后散步走回家，其中 x 表示时间，y 表示张强离家的距离。根据图象提供的信息，以下四个说法错误的是（ ）
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
