练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

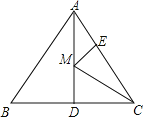
    【题目】如图，等边△ABC的边长为6，AD是BC边上的中线，M是AD上的动点，E是AC边上一点，若AE=2，EM+CM的最小值为______．

    【答案】．

    【解析】试题分析：连接BE，与AD交于点M．则BE就是EM+CM的最小值．

    取CE中点F，连接DF．

    ∵等边△ABC的边长为6，AE=2，∴CE=AC﹣AE=6﹣2=4，∴CF=EF=AE=2，又∵AD是BC边上的中线，∴DF是△BCE的中位线，∴BE=2DF，BE∥DF，又∵E为AF的中点，∴M为AD的中点，∴ME是△ADF的中位线，∴DF=2ME，∴BE=2DF=4ME，∴BM=BE﹣ME=4ME﹣ME=3ME，∴BE=BM．在直角△BDM中，BD=BC=3，DM=AD=，∴BM==，∴BE==．∵EM+CM=BE，∴EM+CM的最小值为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我们可以用几何图形来解决一些代数问题，如图（甲）可以来解释（a+b）2=a2+2ab+b2，

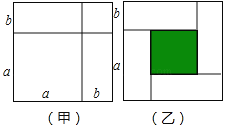
    （1）图（乙）是四张全等的矩形纸片拼成的图形，请利用图中阴影部分面积的不同表示方法，写出一个关于a，b代数恒等式表示 ；

    （2）请构图解释：（a+b+c）2=a2+b2+c2+2ab+2bc+2ac；

    （3）请通过构图因式分解：a2+3ab+2b2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是( )

    A. 2x2·2xy＝4x3y4 B. 3x2y－5xy2＝－2x2y

    C. x－1÷x－2＝x－1 D. (－3a－2)(－3a＋2)＝9a2－4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点P（m，m﹣2）不可能在第　 　象限．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

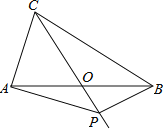
    【题目】如图，在等腰△ABC中，AB=BC=4，点O是AB的中点，∠AOC=60°，点P是射线CO上的一个动点，若当△PAB为直角三角线时，试画出可能的图形（两种即可），并求出相应图形中的AP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】函数y=mx－(m－2)的图象经过点（0，3）,则m=______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算（a﹣1）（2a+1）＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是（ ）
    A.a+a=a2
    B.（2a）3=6a3
    C.（a﹣1）2=a2﹣1
    D.a3÷a=a2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一副三角板的直角重合放置，如图1所示，

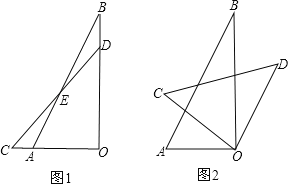
    （1）图1中∠BEC的度数为_________

    （2）三角板△AOB的位置保持不动，将三角板△COD绕其直角顶点O顺时针方向旋转：

    ①当旋转至图2所示位置时，恰好OD∥AB，求此时∠AOC的大小；

    ②若将三角板△COD继续绕O旋转，直至回到图1位置，在这一过程中，是否会存在△COD其中一边能与AB平行？如果存在，请你画出图形，并直接写出相应的∠AOC的大小；如果不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案