
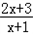 (x>﹣1)中的y的取值范围.
(x>﹣1)中的y的取值范围.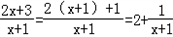
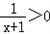
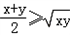 (x、y为正数);此不等式说明:当正数x、y的积为定值时,其和有最小值.
(x、y为正数);此不等式说明:当正数x、y的积为定值时,其和有最小值. ≥2(x>0)
≥2(x>0)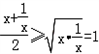
 ≥2利用以上信息,解决以下问题:
≥2利用以上信息,解决以下问题: 中(x>1),y的取值范围是( );
中(x>1),y的取值范围是( ); 的最小值是( ).
的最小值是( ).科目:初中数学 来源: 题型:阅读理解
|
| a2 |
| a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
|
| a2 |
| a2 |
| a2 |
| (x-2)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
|
| a2 |
| a2 |
| (x-5)2 |
| (x+3)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 时,如
时,如 则
则 ,故此时
,故此时 的绝对值是它本身
的绝对值是它本身 时,
时, ,故此时
,故此时 的绝对值是零
的绝对值是零 时,如
时,如 则
则 ,故此时
,故此时 的绝对值是它的相反数
的绝对值是它的相反数 综合起来一个数的绝对值要分三种情况,即
综合起来一个数的绝对值要分三种情况,即
 的各种展开的情况.
的各种展开的情况. (3)猜想
(3)猜想 与
与 的大小关系.
的大小关系.
查看答案和解析>>
科目:初中数学 来源:2010年辽宁省大连市第十四中学初二数学阶段性检测数学卷 题型:解答题
(12分)阅读材料,解答下列问题.
例:当 时,如
时,如 则
则 ,故此时
,故此时 的绝对值是它本身
的绝对值是它本身
当 时,
时, ,故此时
,故此时 的绝对值是零
的绝对值是零
当 时,如
时,如 则
则 ,故此时
,故此时 的绝对值是它的相反数
的绝对值是它的相反数 综合起来一个数的绝对值要分三种情况,即
综合起来一个数的绝对值要分三种情况,即
问:(1)这种分析方法涌透了 数学思想.
(2)请仿照例中的分类讨论的方法,分析二次根式 的各种展开的情况.
的各种展开的情况. (3)猜想
(3)猜想 与
与 的大小关系.
的大小关系.
(4)尝试用从以上探究中得到的结论来解决下面的问题: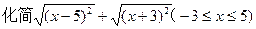
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com