
分析 首先将方程两边通分,然后再根据化简后方程的特点,去分母转换为整式方程求解.
解答 解:原方程转化为:1+$\frac{1}{x+1}+1+\frac{1}{x+7}=1+\frac{1}{x+5}+1+\frac{1}{x+3}$
$\frac{1}{x+1}+\frac{1}{x+7}=\frac{1}{x+5}+\frac{1}{x+3}$
$\frac{1}{x+1}$-$\frac{1}{x+3}$=$\frac{1}{x+5}$-$\frac{1}{x+7}$,
整理得:$\frac{1}{(x+1)(x+3)}=\frac{1}{(x+5)(x+7)}$
去分母得:(x+5)(x+7)=(x+1)(x+3),
即:x2+12x+35=x2+4x+3,解得x=-4;
经检验,x=-4是原方程的解.
点评 此题考查的是解分式方程的方法和步骤;将方程经过适当变形后,还是可以将其视为普通的分式方程进行求解,熟练掌握分式方程的基本解法是解决问题的关键.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
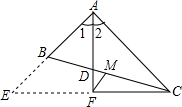 在△ABC中,AC>AB,M为BC的中点.AD是∠BAC的平分线,若CF⊥AD交AD的延长线于F.求证:MF=$\frac{1}{2}$﹙AC-AB﹚.
在△ABC中,AC>AB,M为BC的中点.AD是∠BAC的平分线,若CF⊥AD交AD的延长线于F.求证:MF=$\frac{1}{2}$﹙AC-AB﹚.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
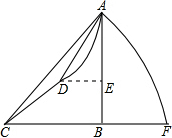 小明在山脚C处测得山顶A的仰角为45°,他沿坡角为37°的斜坡前进200米到达D处,测得山顶A的仰角为53°,求山高AB(A、B、C、D、E、F在一个平面内)参考数据:sin37°=cos53°≈$\frac{3}{5}$,cos37°=sin53°≈$\frac{4}{5}$,tan53°≈$\frac{4}{3}$.
小明在山脚C处测得山顶A的仰角为45°,他沿坡角为37°的斜坡前进200米到达D处,测得山顶A的仰角为53°,求山高AB(A、B、C、D、E、F在一个平面内)参考数据:sin37°=cos53°≈$\frac{3}{5}$,cos37°=sin53°≈$\frac{4}{5}$,tan53°≈$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
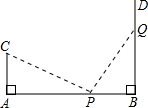 如图,AB=12米,CA⊥AB于A,DB⊥AB于B,且AC=4米,P点从B向A运动,每分钟走1米,Q点从B向D运动,每分钟走2米,P、Q两点同时出发,运动几分钟后,△CAP≌△PBQ?试说明理由.
如图,AB=12米,CA⊥AB于A,DB⊥AB于B,且AC=4米,P点从B向A运动,每分钟走1米,Q点从B向D运动,每分钟走2米,P、Q两点同时出发,运动几分钟后,△CAP≌△PBQ?试说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com