
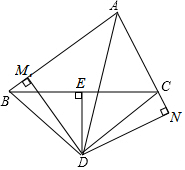
 如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC的延长线于点N,下列结论中错误的是( )
如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC的延长线于点N,下列结论中错误的是( )| A. | DM=DN | B. | ∠ABD+∠ACD=180° | ||
| C. | AC+AN=AB | D. | BC2+4DE2=4BM2+4DM2 |
分析 根据角平分线的性质和线段垂直平分线的性质可得到DM=DN,DB=DC,根据HL证明△DMB≌△DNC,即可得出DM=DN,根据四边形的内角和得到∠ABD+∠ACD=180°;根据勾股定理得到BC2+4DE2=4BM2+4DM2;由于AC不一定等于BM,得到AC+AN不一定等于AB,于是得到结论.
解答 证明:连接BD,
∵AD是∠CAB的平分线,DM⊥AB,DN⊥AC,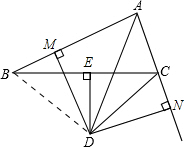
∴DM=DN,
∵DE垂直平分线BC,
∴DB=DC,
在Rt△DMB和Rt△DNC中,$\left\{\begin{array}{l}{DB=DC}\\{DM=DN}\end{array}\right.$,
∴Rt△DMB≌Rt△DNC(HL),
∴DM=DN,故A正确;∠BDM=∠CDN,
∴∠MDN=∠CDB,
∵∠BAC+∠MDN=360°-∠AMD-∠AND=180°,
∴∠ABD+∠ACD=180°;故B正确;
∵DE垂直平分线BC,
∴DE⊥BC,BC=2BE=2CE,
∴BC2+4DE2=(2BE)2+4DE2=4BE2+4DE2=4(BE2+DE2),
∵BD2=BM2+DM2=DE2+BE2,
∴BC2+4DE2=4BM2+4DM2;故C正确;
∵AM=AN,但AC不一定等于BM,
∴AC+AN不一定等于AB,故C错误,
故选C.
点评 本题主要考查了角平分线的性质和线段垂直平分线的性质以及全等三角形的判定与性质,熟悉角平分线的性质和线段垂直平分线的性质是解决问题的关键.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
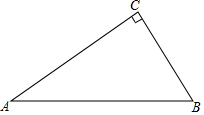 如图.△ABC是直角三角形,∠ACB=90°,∠A=30°.
如图.△ABC是直角三角形,∠ACB=90°,∠A=30°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
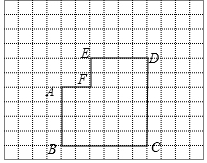 下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.
下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5×10-7毫米2 | B. | 5×10-8毫米2 | C. | 2×106毫米2 | D. | 2×107毫米2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
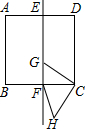 如图,正方形ABCD的边长为6,EF为正方形ABCD的对称轴,交BC于F点,点G是对称轴EF上的一个动点,连接GC,将线段GC绕点C逆时针旋转90°得到HC,连接HF,则在点G运动过程中,HF的最小值是( )
如图,正方形ABCD的边长为6,EF为正方形ABCD的对称轴,交BC于F点,点G是对称轴EF上的一个动点,连接GC,将线段GC绕点C逆时针旋转90°得到HC,连接HF,则在点G运动过程中,HF的最小值是( )| A. | $\frac{1}{2}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
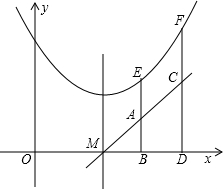 如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )
如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )| A. | S=y2+y1 | B. | S=y2+2y1 | C. | S=y2-y1 | D. | S=y2-2y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
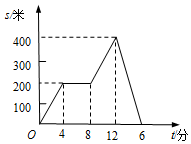 小明从家出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步一段时间,然后回家.图中描述了小明在散步过程中到家的距离s(m)与散步所用时间t(min)之间的函数关系,则小明看报用了4min;小明返回家时的平均速度是100m/min.
小明从家出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步一段时间,然后回家.图中描述了小明在散步过程中到家的距离s(m)与散步所用时间t(min)之间的函数关系,则小明看报用了4min;小明返回家时的平均速度是100m/min.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com