
 如图,BD是△ABC的角平分线,它的垂直平分线分别交AB、BC于点E、F、G,连接ED、DG.
如图,BD是△ABC的角平分线,它的垂直平分线分别交AB、BC于点E、F、G,连接ED、DG.分析 (1)结论四边形EBGD是菱形.只要证明BE=ED=DG=GB即可.
(2)作DH⊥BC于H,由四边形EBGD为菱形ED=DG=2,求出GH,CH即可解决问题.
解答 解:(1)四边形EBGD是菱形.
理由:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
$\left\{\begin{array}{l}{∠EDF=∠GBF}\\{∠EFD=∠GFB}\\{DF=BF}\end{array}\right.$,
∴△EFD≌△GFB,
∴ED=BG,
∴BE=ED=DG=GB,
∴四边形EBGD是菱形.
(2)作DH⊥BC于H,
∵四边形EBGD为菱形ED=DG=2,
∴∠ABC=30°,∠DGH=30°,
∴DH=1,GH=$\sqrt{3}$,
∵∠C=45°,
∴DH=CH=1,
∴CG=GH+CH=1+$\sqrt{3}$.
点评 本题考查平行四边形的判定和性质、菱形的判定和性质、角平分线的性质、垂直平分线的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造直角三角形解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 分组 | 31-35kg | 36-40kg | 41-45kg | 46-50kg | 51-55kg |
| 人数 | 8 | 23 | 15 | 9 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图数轴上表示的是下列哪个不等式组的解集( )
如图数轴上表示的是下列哪个不等式组的解集( )| A. | $\left\{\begin{array}{l}x>-2\\ x≤3\end{array}\right.$ | B. | $\left\{\begin{array}{l}x≥-2\\ x<3\end{array}\right.$ | C. | $\left\{\begin{array}{l}x<-2\\ x≥3\end{array}\right.$ | D. | $\left\{\begin{array}{l}x≤-2\\ x>3\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
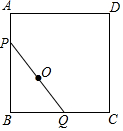 如图,以AB为边作正方形ABCD,动点P、Q分别在AB和BC边上运动,且PQ=AB=8,若点Q从点B出发,沿BC向点C运动,则点P随之沿AB下滑,当B到达C点时停止运动.则点Q从B到C的运动过程中,PQ的中点O所经过的路径长为2π.
如图,以AB为边作正方形ABCD,动点P、Q分别在AB和BC边上运动,且PQ=AB=8,若点Q从点B出发,沿BC向点C运动,则点P随之沿AB下滑,当B到达C点时停止运动.则点Q从B到C的运动过程中,PQ的中点O所经过的路径长为2π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com