
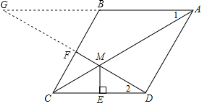
【题目】已知:如图,在菱形![]() 中,
中,![]() 为边
为边![]() 的中点,
的中点,![]() 与对角线
与对角线![]() 交于点
交于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,![]() .
.
![]() 若
若![]() ,求
,求![]() 的长;
的长;
![]() 求证:
求证:![]() .
.

【答案】(1)2;(2)见解析
【解析】
(1)根据菱形的对边平行可得AB∥CD,再根据两直线平行,内错角相等可得∠1=∠ACD,所以∠ACD=∠2,根据等角对等边的性质可得CM=DM,再根据等腰三角形三线合一的性质可得CE=DE,然后求出CD的长度,即为菱形的边长BC的长度;
(2)先利用“边角边”证明△CEM和△CFM全等,根据全等三角形对应边相等可得ME=MF,延长AB交DF于点G,然后证明∠1=∠G,根据等角对等边的性质可得AM=GM,再利用“角角边”证明△CDF和△BGF全等,根据全等三角形对应边相等可得GF=DF,最后结合图形GM=GF+MF即可得证.
解:![]() 解:∵四边形
解:∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 证明:∵
证明:∵![]() 为边
为边![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
在菱形![]() 中,
中,![]() 平分
平分![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵ ,
,
∴![]() ,
,
∴![]() ,
,
延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵ ,
,
∴![]() ,
,
∴![]() ,
,
由图形可知,![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
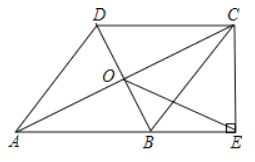
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,对角线
,对角线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 平分
平分![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)如图2,在(1)的条件下,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庆元大道两侧需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积S(单位m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
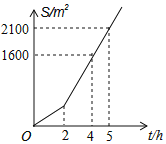
A. 200B. 300C. 400D. 500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,CE是∠DCB的平分线,F是AB的中点,AB=6,BC=5,则AE:EF:FB为( )

A. 1:2:3 B. 2:1:3 C. 3:2:1 D. 3:1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,M、N分别是边AD、BC边上的中点,且△ABM≌△DCM;E、F分别是线段BM、CM的中点.
(1)求证:平行四边形ABCD是矩形.
(2)求证:EF与MN互相垂直.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,则①CA平分∠BCD;②AC⊥BD;③∠ABC=∠ADC=90°;④四边形ABCD的面积为ACBD.上述结论正确的个数是( )

A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
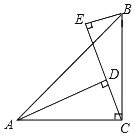
【题目】已知:如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D,E.
(1)求证:△BEC≌△CDA;
(2)当AD=3,BE=1时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,
(1)问应将每件售价定为多少元时,才能使每天利润为640元且成本最少?
(2)问应将每件售价定为多少元时,才能使每天利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com