【题目】尺规作图：作点A关于直线l的对称点A'.
已知：直线l和l外一点A.
求作：点A关于l的对称点A'.
作法：①在l上任取一点P，以点P为圆心，PA长为半径作孤，交l于点B；②以点B为圆心，AB长为半径作弧，交弧AB于点A'. 点A'就是所求作的对称点.
由步骤①，得________
由步骤②，得________
将横线上的内容填写完整，并说明点A与A'关于直线l对称的理由________.
【答案】PA=PB ；AB=BA' ；根据线段相等，即可证明三角形全等，证明对称 .
【解析】
由①的作图步骤可知A和B均为以P为圆心的圆上，所以PA和PB都为园的半径相等；
由②同理也可知A'既在以P为圆心的圆上也在以B为圆心的圆上，所以AB= A'B，P A'=PB=PA，可知三角形APB≌三角形A'PB，所以A与A'关于直线l对称.
解：由①的作图步骤可知A和B均为以P为圆心的圆上，所以PA和PB都为园的半径相等；由②同理也可知A'既在以P为圆心的圆上也在以B为圆心的圆上，所以AB= A'B，P A'=PB=PA，而PB为三角形APB、三角形A'PB的共边，可知三角形APB≌三角形A'PB，所以A与A'关于直线l对称.
科目：初中数学 来源： 题型：
【题目】某地震救援队探测出某建筑物废墟下方点C处有生命迹象，已知废墟一侧地面上两探测点A，B相距3米，探测线与地面的夹角分别是30°和60°（如图），试确定生命所在点C的深度．（结果保留根号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请认真观察如下图形：
当
时，长方形
分为2个直角三角形；
当
时，长方形分为8个直角三角形；
当
时，长方形分为18个直角三角形；
……
依此规律，第
个图形中，长方形被分成______个小直角三角形.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题再现：
数形结合是一种重要的数学思想方法，借助这种思想方法可将抽象的数学知识变得直观并且具有可操作性.初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如：利用图形的几何意义验证完全平方公式.
将一个边长为
的正方形的边长增加
，形成两个长方形和两个正方形，如图所示：这个图形的面积可以表示成：
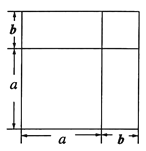
或
∴
这就验证了两数和的完全平方公式.
类比解决：
请你类比上述方法，利用图形的几何意义验证平方差公式.
（要求画出图形并写出推理过程）
问题提出：如何利用图形几何意义的方法证明
？
如图所示，
表示1个1×1的正方形，即：
，
表示1个2×2的正方形，
与
恰好可以拼成1个2×2的正方形，因此：、、就可以表示2个2×2的正方形，即：
而、、、恰好可以拼成一个
的大正方形.
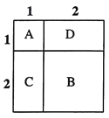
由此可得：
.
尝试解决：
请你类比上述推导过程，利用图形的几何意义确定：
_______.（要求写出结论并构造图形写出推证过程）.
问题拓广：
请用上面的表示几何图形面积的方法探究：
_______.（直接写出结论即可，不必写出解题过程）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是矩形，对角线AC的垂直平分线EF交AC于O，分别交BC、AD于点E、F．
（1）求证：四边形AECF是菱形；
（2）若AB=4，BC=8，求EC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】周末，小梅骑自行车去外婆家，从家出发
小时后到达甲地，在甲地游玩一段时间后，按原速继续前进，小梅出发
小时后，爸爸骑摩托车沿小梅骑自行车的路线追赶小梅，如图是他们离家的路程
（千米）与小梅离家时间
（小时）的关系图，已知爸爸骑摩托车的速度是小梅骑自行车速度的
倍。
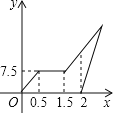
（1）小梅在甲地游玩时间是_________小时，小梅骑车的速度是_________千米/小时.
（2）若爸爸与小梅同时到达外婆家，求小梅家到外婆家的路程.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某汽车专卖店销售A，B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元.
（1）求每辆A型车和B型车的售价各为多少万元？
（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，且A型号车不少于2辆，购车费不少于130万元，则有哪几种购车方案？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在大棚中栽培新品种的蘑菇，在18℃的条件下生长最快，因此用装有恒温系统的大棚栽培，如图是某天恒温系统从开启升温到保持恒温及关闭．大棚内温度y（℃）随时间x（时）变化的函数图像，其中BC段是函数y＝
（k＞0）图像的一部分．
（1）分别求出0≤x≤2和x≥12时对应的y与x的函数关系式；
（2）若该蘑菇适宜生长的温度不低于12℃，则这天该种蘑菇适宜生长的时间是多长？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
