
【题目】已知二次函数y=﹣![]() x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.
x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.
(1)用b的代数式表示顶点M的坐标;
(2)当tan∠MAN=2时,求此二次函数的解析式及∠ACB的正切值.

【答案】(1)M(![]() ,
, ![]() );(2)
);(2)![]() ,
, ![]()
【解析】试题分析:把点A(2,0)坐标代入二次函数![]() 解析式得出
解析式得出![]() ,再带回到
,再带回到![]() 中,配方化为顶点式即可得到顶点M的坐标;(2)先由tan∠MAN=2得出MN的长度,再分类讨论点B和N的位置关系,得出b的值,进而得出二次函数的解析式,A作AH⊥BC,根据正切函数定义即可得出∠ACB的正切值
中,配方化为顶点式即可得到顶点M的坐标;(2)先由tan∠MAN=2得出MN的长度,再分类讨论点B和N的位置关系,得出b的值,进而得出二次函数的解析式,A作AH⊥BC,根据正切函数定义即可得出∠ACB的正切值
解:(1)∵二次函数![]() 的图像经过点A(2,0),
的图像经过点A(2,0),
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴顶点M的坐标为(![]() ,
, ![]() ).
).
(2)∵tan∠MAN=![]() 2,∴MN=2AN.
2,∴MN=2AN.
∵M(![]() ,
, ![]() ),∴ N(
),∴ N(![]() ,0),
,0),![]() .
.
①当点B在点N左侧时, AN= ![]() ,∴
,∴![]() ,
, ![]() .
.
不符合题意.
②当点B在点N右侧时, AN= ![]() , ∴
, ∴![]() ,
, ![]() .
.
∴二次函数的解析式为![]() .
.
∴点C(0,–10),∵点A、B关于直线MN对称,∴点B(10,0).
∵OB=OC=10,∴BC=10![]() ,∠OBC=45°.
,∠OBC=45°.
过点A作AH⊥BC,垂足为H,∵AB=8,∴AH=BH=4![]() ,∴CH=6
,∴CH=6![]() .
.
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
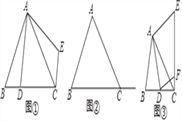
【题目】在△ABC中,∠ACB是锐角,点D在射线BC上运动,连接AD,将线段AD绕点A逆时针旋转90°,得到AE,连接EC.
(1)操作发现:若AB=AC,∠BAC=90°,当D在线段BC上时(不与点B重合),如图①所示,请你直接写出线段CE和BD的位置关系和数量关系是_____,_____;
(2)猜想论证:
在(1)的条件下,当D在线段BC的延长线上时,如图②所示,请你判断(1)中结论是否成立,并证明你的判断.
(3)拓展延伸:
如图③,若AB≠AC,∠BAC≠90°,点D在线段BC上运动,试探究:当锐角∠ACB等于_____度时,线段CE和BD之间的位置关系仍成立(点C、E重合除外)?此时若作DF⊥AD交线段CE于点F,且当AC=3![]() 时,请直接写出线段CF的长的最大值是_____
时,请直接写出线段CF的长的最大值是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校新到一批理、化、生实验器材需要整理,若实验管理员李老师一人单独整理需要40分钟完成,现在李老师与工人王师傅共同整理20分钟后,李老师因事外出,王师傅再单独整理了20分钟才完成任务.
(1)王师傅单独整理这批实验器材需要多少分钟?
(2)学校要求王师傅的工作时间不能超过30分钟,要完成整理这批器材,李老师至少要工作多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,BC=3,AB=4,D是边AB上一点,DE∥BC交AC于点E,将△ADE沿DE翻折得到△A′DE,若△A′EC是直角三角形,则AD长为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A. 4cmB. 2cm;C. 小于2cmD. 不大于2cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com