
 如图,在边长为4的正方形ABCD中,M为边AB上的点,且AM=$\frac{1}{3}$BM,延长MB至点E,使ME=MC,连接EC,则点M到直线CE的距离是( )
如图,在边长为4的正方形ABCD中,M为边AB上的点,且AM=$\frac{1}{3}$BM,延长MB至点E,使ME=MC,连接EC,则点M到直线CE的距离是( )| A. | 2 | B. | $\sqrt{5}$ | C. | 5 | D. | 2$\sqrt{5}$ |
分析 如图,作MN⊥EC于N.首先利用勾股定理求出CM、CE,再根据$\frac{1}{2}$ME•CB=$\frac{1}{2}$CE•MN,即可解决问题.
解答 解:如图,作MN⊥EC于N.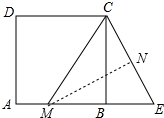
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,∠ABC=90°,
∴AM=$\frac{1}{3}$BM,
∴AM=1,BM=3,
在Rt△BCM中,CM=ME=$\sqrt{B{M}^{2}+C{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴BE=5-3=2,
∴CE=$\sqrt{B{C}^{2}+B{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$
∵$\frac{1}{2}$ME•CB=$\frac{1}{2}$CE•MN,
∴MN=$\frac{ME•BC}{CE}$=$\frac{5×4}{2\sqrt{5}}$=2$\sqrt{5}$,
故选D.
点评 本题考查正方形的性质、勾股定理、三角形的面积公式、点到直线的距离等知识,解题的关键是灵活运用勾股定理,学会利用等积法求高,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| 时间(年) | 1949 | 1959 | 1969 | 1979 | 1989 | 1999 |
| 人口(亿) | 5.42 | 6.72 | 8.07 | 9.75 | 11.07 | 12.59 |
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
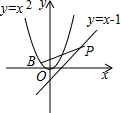 如图,点P在直线y=x-1上,若存在过点P的直线交抛物线y=x2于A、B两点,且PA=AB,则称点P为“优点”,下列结论中正确的是( )
如图,点P在直线y=x-1上,若存在过点P的直线交抛物线y=x2于A、B两点,且PA=AB,则称点P为“优点”,下列结论中正确的是( )| A. | 直线y=x-1上的所有点都是“优点” | |
| B. | 直线y=x-1上仅有有限个点是“优点” | |
| C. | 直线y=x-1上的所有点都不是“优点” | |
| D. | 直线y=x-1上有无穷多个点(不是所有的点)是“优点” |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,两人从路段AB上一点C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地.且DA⊥AB,EB⊥AB.若线段DA=EB相等,则C是路段AB的中点吗?为什么?
如图,两人从路段AB上一点C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地.且DA⊥AB,EB⊥AB.若线段DA=EB相等,则C是路段AB的中点吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我市某中学开设“生物第二课堂”,在校园内开辟出一块L型的空闲土地,准备进行植物种植研究,按如图所示的虚线分成了面积相等的两个梯形,这两个梯形的上底都是am,下底都是bm,高都是(b-a)m,请你算一算这块土地的面积是多少?并求出当a=20m,b=30m时这块土地的面积.
我市某中学开设“生物第二课堂”,在校园内开辟出一块L型的空闲土地,准备进行植物种植研究,按如图所示的虚线分成了面积相等的两个梯形,这两个梯形的上底都是am,下底都是bm,高都是(b-a)m,请你算一算这块土地的面积是多少?并求出当a=20m,b=30m时这块土地的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com