
【题目】如图,在△ABC中,点D是边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE.
(1)求证:DE=DF;
(2)当∠A=90°时,试判断四边形AFDE是怎样的四边形,并证明你的结论.
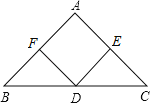
【答案】(1)证明见解析;(2)四边形AFDE是正方形.理由见解析.
【解析】
试题
(1)由已知条件可由“HL”证Rt△DBF≌Rt△DCE,从而可得:DE=DF;
(2)由∠A=∠DFA=∠DEA=90°可证得四边形AFDE是矩形,结合DF=DE,可得四边形AFDE是正方形.
试题解析:
(1)∵D是BC的中点,
∴BD=CD,
∵DE⊥AC,DF⊥AB,
∴∠BFD=∠CED=90°,
在Rt△BDF和Rt△CDE中,![]() ,
,
∴Rt△BDF≌Rt△CDE(HL),
∴DE=DF;
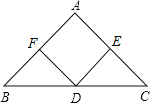
(2)当∠A=90°时,四边形AFDE是正方形.理由如下:
∵DE⊥AC,DF⊥AB,
∴∠DEA=∠DFA=90°,
又∵∠A=90°,
∴四边形AFDE是矩形,
又∵DF=DE,
∴四边形AFDE是正方形.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小贤与小杰在探究某类二次函数问题时,经历了如下过程:
求解体验:
(1)已知抛物线y=﹣x2+bx﹣3经过点(﹣1,0),则b= ,顶点坐标 ,该抛物线关于点(0,1)成中心对称的抛物线的表达式是 .
抽象感悟:
我们定义:对于抛物线y=ax2+bx+c(a≠0),以y轴上的点M(0,m)为中心,作该抛物线关于点M对称的抛物线y',则我们又称抛物线y'为抛物线y的“衍生抛物线”,点M为“衍生中心”.
(2)已知抛物线y=﹣x2﹣2x+5关于点(0,m)的衍生抛物线为y',若这两条抛物线有交点,求m的取值范围.
问题解决:
(3)已知抛物线y=ax2+2ax﹣b(a≠0)若抛物线y的衍生抛物线为y'=bx2﹣2bx+a2(b≠0),两抛物线有两个交点,且恰好是它们的顶点,求a,b的值及衍生中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
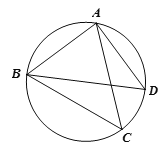
【题目】如图,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究![]() ,
,![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为12cm,点B,D之间的距离为16m,则线段AB的长为![]()
![]()
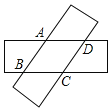
A. ![]() B. 10cmC. 20cmD. 12cm
B. 10cmC. 20cmD. 12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+2x﹣3与x轴交于A,B两点(点A在点B的左侧),将这条抛物线向右平移m(m>0)个单位长度,平移后的抛物线与x轴交于C,D两点(点C在点D的左侧),若B,C是线段AD的三等分点,则m的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
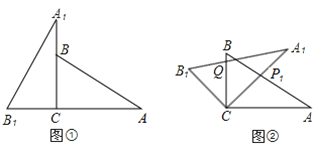
【题目】将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com